【解法紹介】自分はこうやって今の解法にたどり着きました ~ にに の場合 ~

☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆

🚨 注意点 🚨
事前準備|9月20日(火)18時00分までに、令和3年度事例Ⅰ、Ⅱ、Ⅲを
それぞれ80分で解き、申し込み受付メールに添付のアンケートフォームに
解答を記入して提出してください。
①参加人数が限られているため申し込み後のキャンセルはお控えください。
②期限までに解答の提出が無い場合はキャンセルとさせていただきます。
③基本的に途中参加、途中退出はお控えください。
④解答は80分で作成したものを提出してください。
先日募集をした道場勉強会、おかげさまで満員のお申し込みをいただいています。
お申し込みくださったかたには、令和3年度事例Ⅰ~Ⅲをそれぞれ80分で問いた解答をお送りくださるようお願いをしています。
その締切が今日の18時に迫ってきています。まだお送りくださっていないかたは、必ず期限までにお送りください!
期限までにお送りいただけなかった場合、大変残念ですがキャンセルとさせていただき、他のかたに席を譲っていただくことになりますので、期限厳守でお願いします!
まえおき
上で勉強会のお知らせをしていますが、少し前の9月4日(日)にも2次試験向けセミナーを開催しました。
200名以上のかたにご参加いただき、大盛況だったのではないかと自負しております。
手前味噌!

サマリー(前半・後半)もこのブログ上で紹介していますので、セミナーに参加できなかったかたも、どういったものだったかは掴んでいただいているのかな、と思います。
セミナーの中では、メンバーそれぞれが何らかのパートを受けもって、自身の知識や経験をお伝えしました。
私にには、今日のこの記事のタイトルと同名の「【解法紹介】自分はこうやって今の解法にたどり着きました」というコーナーで、りいあ・どらごんとともに、解法についてお話ししました。
お話をしたあと、セミナーに参加された何人かのかたから、

参考になりました
一般的な解法でうまく解くことができず悩んでいたので、違うやり方でやってもいいんだって勇気づけられました
みたいな、とてもありがたい声をかけていただきました。
また、セミナー終了後にお願いしたアンケートでも、やはり幾人かのかたから同様のご感想を頂戴しています。
私の解法は、後半で詳しくお伝えしますが、いわゆる王道と言われるような一般的なやり方とはだいぶ違っています。
そんな特殊なやり方を紹介しても役に立たないのではないか、という思いもあったのですが、実際は上記のように、何かしらプラスに捉えてくださるかたもいらっしゃいました。
というわけで、セミナーにご参加いただけなかったかたにも、同じように何かしらを感じていただけるのではないかと思い、セミナーでお話しした内容をブログでもご紹介することにしました。
セミナーにご参加されたかたも、復習がてらご覧ください!
前置きが長くなりましたが、以下本題に入ります☆
私の解法(最終形)
私の、および道場13代目全員の解法については、以前インタビューリレーでhotmanがまとめてくれています。そのときのまとめの画像を再掲します。
自信作やで

画像の左側がいわゆる王道に近い解法で、私は見事右側(どらごん以降)の「奇行種」ゾーンの一角を占めています。

私の解法の変遷
最初は普通の方法を志向/試行した
こんな感じで奇行種っぷり全開の私の解法ですが、最初からこうだったわけではありません。最初は、いわゆる王道の方法でやってみようと思い、実際にしばらくそれで試行錯誤していました。
最初に志向した方法と、最終的な方法を比べてみたのが以下の表です。
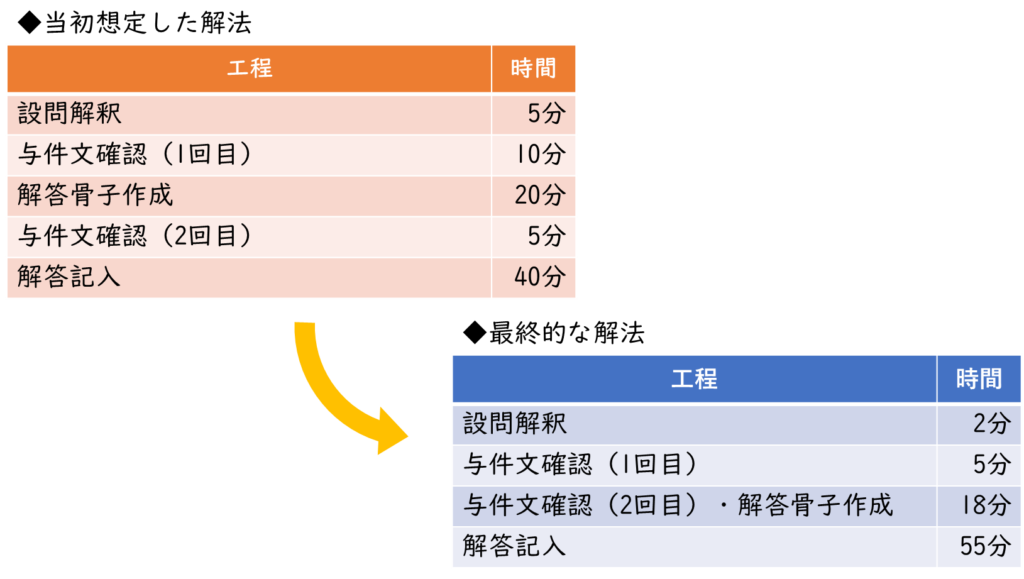

~お詫びと訂正~
セミナーでも使用したこの表ですが、セミナー資料では「与件文確認(2回目)・解答骨子作成」の18分を「13分」と誤って記載していました。この場を借りて、謹んでお詫びと訂正を申し上げます。
足し算ができなかったんです!
hotmanの表は正しい時間です!

アカーーーン!
当初は、左側の王道に近い方法をしばらく試していましたが、これがどうにもしっくり来ず、また時間も80分に収めることができない、という状態が続きました。
というわけで、方法の改善を試みることになるわけです。
以下、いくつかの変更点をご紹介していきますが、もちろん一度にすべて変えたわけではありません。
徐々に変えていって最終的にこうなった、というのが先ほどご紹介した方法ですが、どの変更をいつやったという時系列は今となっては闇の中(覚えてない)です。
なので、お読みになっているあなたがもし、仮に、万が一参考にしてくださる場合も、それぞれの工程をどう検討してどう判断したか、そこを見ていただければと思います。
くれぐれも、私の最終的な解法をなぞってそのまま試すという暴挙にはお出になりませぬよう、お願いします。
手順の改善
手順を細分化し、問題点を抽出する
というわけで、方法を改善するために、まずは手順を細分化してみました。セミナーのときお見せしたのと同じですが、こういった形になりました。
そして、スライドの2枚目に、それぞれの工程がしっくりくるかどうかを判定した結果を示しています。


ご覧のとおり、ダメ工程がかなり多いです。
あくまでも、「当時の私が80分でそれなりの解答にたどり着くためには」ダメだった、ということは強調しておきたいと思います。
これから手順を修正していくわけですが、方法の改善といえば、そうですね、ECRSの法則です。
突然ですが穴埋め問題にしてみたので、覚えているかどうか、確認してみてください。1次知識ではありますが、2次試験の事例Ⅲにおいてもフレームワークのひとつとして覚えておいて損はないと思います。(選択して反転させると答えが見えます)
| 略字 | 英語 | 意味 |
|---|---|---|
| E | Eliminate | 削減する |
| C | Combine | 結合する |
| R | Rearrange | 入れ替える |
| S | Simplify | 単純化する |
それでは、ECRSの法則にのっとって、ダメ工程を改善していきましょう。
設問解釈
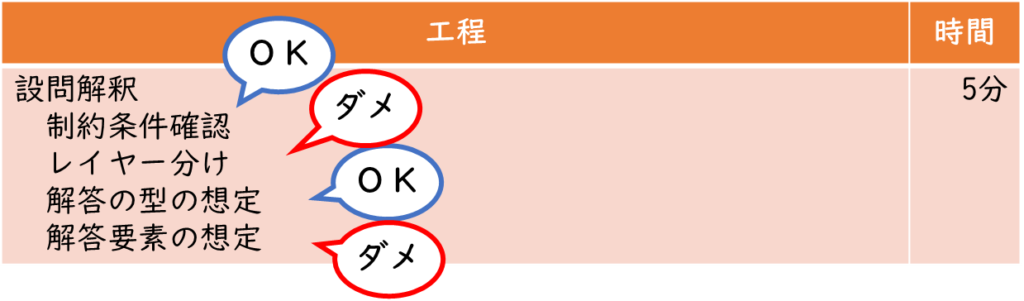
設問解釈の中では、2つの工程「レイヤーを判断する」と「解答要素を想定する」が、改善の対象となりました。
- レイヤーを判断する → Eliminate(削減する)
この工程については、当時の私は「レイヤーを判断して、で、それでどうするの?」と思っていました。
論点を大外しするのを避けるためだけのものと思っていて、しばらく過去問を解いてみた結果そこを外すことはなかったので、この「レイヤーを判断する」という工程はなくしても問題ないと判断しました。
ちなみに今は、2次プロジェクトなど有用な記事もたくさん見ていますので、もう少し前向きにレイヤーを使いこなすこともできるんじゃないかと思っています。
- 解答要素を想定する → Eliminate(削減する)
この工程は、精度良く行なうことができれば、再現性・安定性を高めることに大きく寄与する、と思います。ですが、当時の私にはそれは難しいものでした。
今思い返してみると、単純に練習不足だったのもありますし、その重要性をちゃんと認識できていなかった故に、「どうせ与件文を見ないと確定できないし」という気持ちがあって精度を高めることができなかったんだろうなぁと思います。
そんなわけで、当時の私にはこの工程を有効に使うことができず、結果Eliminateするという判断をしました。
与件文確認(1回目)

ここの工程は、人それぞれやり方があって、今もいろいろ悩んでいるというかたも多いのではないでしょうか。
私も当初、設問文をしっかり把握したあと与件文を読んで、設問ごとに解答に使えそうな要素を色を変えてマーキングして・・・と思っていました。
ですが、今思うとこの工程がもっとも私に合っていなかったようです。試してはみたものの、とてもやりづらく、時間もかかり、そのうえ解答の質も上がらず、といった散々なものでした。
それは、主に2つのことが原因でした。
- 原因1:設問文の内容を覚えていない
もっとも大きな原因はこれでした。与件文を読みながら、

あ、これ解答に使えそう

・・・第何問だっけ?
ということが頻発して、与件文と設問文を行ったり来たり。時間がかかって仕方がありませんでした。
- 原因2:後からマーカーを追加することも多く、付番がごちゃごちゃになる

解答要素に付番することについては、その付番がごちゃごちゃになるという問題もありました。この画像のように、後から気づいて1番の上に6番を書き加える、というのが典型的な例です。
こうなってくると、「今何番まで使ってるんだっけ?」「○番ってメモに書いてあるけど、与件文のどこ?」といった具合で、混乱はますます深まる結果となりました。
以上の2点を解決するために私がとった方法は、この段階では色分けも付番もやめるということでした。ただ単純に、解答要素になりそうだなと思ったところに鉛筆で線を引くだけにしました。
- 設問ごとに色分けして解答要素にマーカー・番号付与 → Simplify(単純化する) → 気になるところに鉛筆でマーキング
解答骨子作成・与件文確認(2回目)
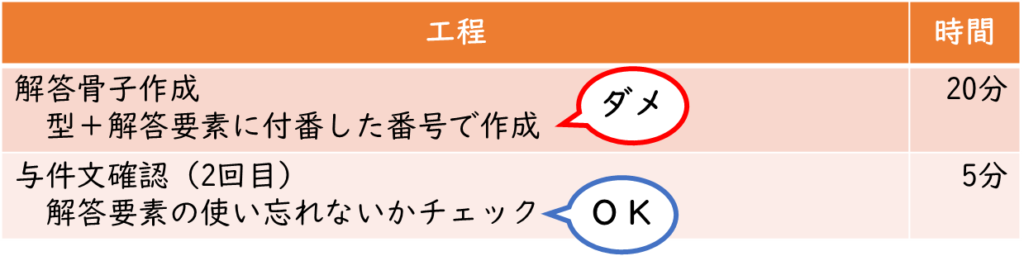
この2つの工程は、当初の想定では「しっかり骨子を作って、そのあと解答要素の使い漏れがないかしっかり確認して」と順を追って進めていくものかな、と思っていました。
ところが、実際やってみるとそんなふうに落ち着き払ってやる余裕はまったくありませんでした。
当初は前工程で付番した番号を使って骨子を作る、という王道の方法を試していましたが、それも私にはしっくりきませんでした。
最大の理由は、 ⑥ だったこと。具体的には① ② 、② ⑤ なため。
みたいに書いても、具体的にイメージすることができなかったんです。
また、前工程で色分けと付番をやめていたこともあり、この工程は最終的に大きく変更することとなりました。
まず、1回目の与件文読み(と鉛筆でのマーキング)のあと、すぐ2回目の与件文読みをすることにしました。2回目はじっくり読むのではなく、設問を1つずつ意識しながらマーキングの箇所だけ拾い読みする感じで進めました。設問の数だけそれを繰り返していたので、実際は「2回目」というより「2~6回目」という方が実態に近いかもしれません。
そうやって設問ごとに解答要素を抽出するのを1次抽出として、次の作業として、1次抽出した要素のうち実際に解答に使うものを2次抽出する、ということを行いました。
その方法は、メモ用紙に書く、です。
先日のセミナーで少しだけお見せした、私が実際に本番で解いた事例Ⅲのメモ用紙部分を掲載します。

・・・聞こえます、あなたの心の声。
・・・これだけ?

そう、これだけなんです。
メモ書きの段階では解答要素の箇条書き(とも言えないくらいの乱雑な殴り書きですが)にとどめ、あとは次の工程にゆだねることにしました。
ちなみに、設問文のページには下線や丸囲みしかしていないので、問題用紙に書いた文字は本当にこれだけです。
なお、解答要素の使い忘れチェックは、すべての設問のメモ書きをひと通り終えたあと、「鉛筆でマーキングしているのに色分けをしていない要素」を確認するという形で行なっていました。
- 型+解答要素に付番した番号で作成・ → Rearrange(入れ替える)・Simplify(単純化する) → 解答要素の抽出・箇条書き
解答記入
そして最後の工程、解答記入です。
ここまでの3つの工程では、いずれもEliminateしたりSimplifyしたりと、手数を減らす方向の改善をしてきました。そうやって節約した時間は、すべてこの工程につぎ込まれることとなりました。
当初40分間を想定していたこの工程の時間は、最終的には55分間まで長くなりました。
そうなった理由は2つあります。
- 理由①:清書したものを見ると直したくなる
前の工程の「付番した番号で骨子を作っても具体的にイメージできない」と通底するものがありますが、実際に解答文として書き上げたものをみると、いろいろ粗が見えてきます。
- 理由②:解答用紙に書いたことしか評価されない
これは、私のオリジナルではなく、受験生時代にどこかで見た言葉です。

ちなみに今回この記事を書くにあたって改めて探してみましたが、見つけることができませんでした💦
まぼろし~☆

どれだけメモ用紙に詳細に書こうとも、それを提出するわけでも採点の対象となるわけでもないので、1点にもなりません。
それならば直接点数につながる解答用紙に時間を使おう、という考えです。(どらごんも同じようなことを言っていますね)
- 骨子に書いてあることを清書 → 逆ECRS → 時間をかけて解答用紙に清書!
私の解法(最終形)のメリデメ・向いている人
メリット
- 書き始めが早い
- 解答用紙に時間を使える
メリットは、書き始めが早いこと、これが一番です。それによって、とりあえず解答用紙を埋めていくことができるので、心の平穏を保ちやすいです。
そしてもう一つ、上でも書いた「解答用紙に書いたことしか評価されない」を踏まえ、得点に直結する解答用紙に時間を使えるということもメリットとして挙げられるでしょう。
デメリット
- 与件文を読んでからの出たとこ勝負になりやすい
- 解答用紙が汚くなる
一方のデメリット、これがあまりにも大きく、私がこの方法をオススメしない最大の理由です。
「与件文を読んでからの出たとこ勝負になりやすい」、つまり、問題によって結果が左右されやすく、安定性に欠けてしまわざるを得ないんです。
とはいえ、当時の私はそもそも安定性という考え方も知らなかったですし、80分以内で解答用紙を書き上げるためにはそのデメリットは受け入れるべきものでした。
おわりに
私の解法についてお話ししてきましたが、冒頭でもお伝えしたとおり、
- この方法そのものはオススメしません
- 手順を変更するにあたって、どんなことを考えたかの参考にしてください
ということは改めて強調しておきたいと思います。
そのうえで、解法がいまいちしっくりこないと思っているあなたが何かを変えるきっかけとして使ってくださるのなら、とてもうれしいです。
あすは まん の2次プロジェクト!レイヤーの使い方など、王道のやり方をお伝えします!
☆☆☆☆☆
いいね!と思っていただけたらぜひ投票(クリック)をお願いします!
ブログを読んでいるみなさんが合格しますように。
にほんブログ村
にほんブログ村のランキングに参加しています。
(クリックしても個人が特定されることはありません)


-1024x661.png)
-1024x661.png)

