【渾身】回帰と機械学習(経営情報システム)【中小企業診断士】
当サイト「中小企業診断士試験 一発合格道場」は、
中小企業診断士試験の合格を目指す方向けに、
代々の合格者が勉強のコツや
診断士としての活動の様子などを書き綴っています。
受験生以外の方も、中小企業診断士という存在に
少しでも興味を持って頂けたら嬉しいです^^
おはようございます。岩塩です。一次試験まで2カ月を切りましたね。初学者の方は過去問には取り組み始めていますか??昨年の私は6/1からTAC過去問集に着手し、約2か月間は過去問を使った鶏ガラ学習法※を行っていましたよ。まだインプット学習を続けている方は、早めに過去問学習を始めましょう!
※鶏ガラ学習法:正しい選択肢を選べたことに満足することなく、設問文・選択肢・解説まで使い倒す学習法。詳しくは初代ハカセの記事で!
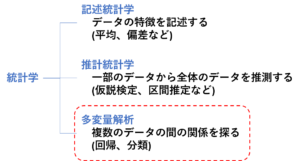
さて、本日は統計学(前回記事)の続編として、回帰と、機械学習を少しを取り上げてみたいと思います。経営情報システムの第20問以降に登場する、後回し推奨な論点ですが、覚えていれば解ける内容も多いので、気になる方はご覧ください。
contents
<回帰>
早速ですが、過去問です。
【H29 情報 第24問】
ある企業では、ここ数年の月当たり販売促進費とその月の売上高を整理したところ、下図のような関係が観察された。 販売促進費と売上高の関係式を求めるための分析手法として、最も適切なものを下記の解答群から選べ。
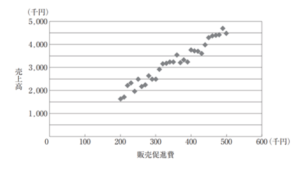
〔解答群〕
ア 因子分析
イ 回帰分析
ウ クラスター分析
エ コンジョイント分析
直球の出題ですが、正解は(イ)の回帰分析です。![]()
この問題では、分析手法の名前が問われただけでしたが、回帰分析について少し深堀りをしてみます。
■単回帰
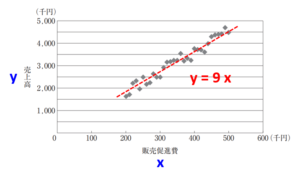
なんとなく、上記のような線が引けそうですよね。販売促進費をx、売上高をyとしてざっくり見積もると、
y=9x・・・①
という直線になりそうです。この式がわかれば、販売促進費から売上高が予測できます。例えば販売促進費を40万円かければ、売上高は360万円くらいになりそうですね。これが回帰分析の基本的な考え方です。
xを説明変数(独立変数)、yを目的変数といいます。このxとyのセットから式を作ることをモデリングといいます。できたy = 9xが回帰モデルです。
①のように説明変数が1つの場合を単回帰分析といいます。
■重回帰
回帰分析では、回帰モデルをうまく作ることが重要です。よいモデルが作れない場合は、精度の高い予測ができません。この問題では、説明変数は販売促進費だけですが、販売促進費だけではうまくモデルが作れない場合もあります。そういう時は、他の説明変数も組み合わせて考えると、よいモデルが作れるかもしれません。例えば以下のような式です。
y = 8x1 + 2x2 + 20・・・②
(y:売上高、x1:販売促進費、x2:広告宣伝費)
販売促進費に加えて、広告宣伝費も説明変数としてみました。販売促進費40万円、広告宣伝費10万円をかければ360万円の売上が上がりそうだな~ということが予測できます。①のように図で説明できるとよいのですが、説明変数が2つ以上になると、二次元のグラフで表せないので、イメージがしにくくなります… (説明変数が2つの場合は、三次元でなんとか表せますが、3つ以上になるともはや認識できません)
②のように2つ以上の場合を重回帰分析といいます。
■回帰モデルを作る手法
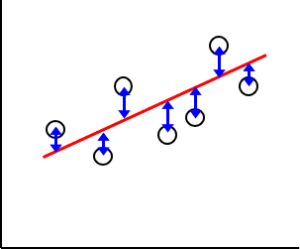
モデルを作るには、xとyの組み合わせを何個か用意して、Excelなどに入力すると、あれやこれやして作ってくれます。彼らは最小二乗法というテクニックで係数を決めていきます。これは、モデル式と各データとの間の距離(下図の青い矢印)を二乗した合計が最小になるようなモデル式を作るやり方です。説明変数が2つ以上の場合や、曲線の場合などもこの方法でモデルを作っていきます。
■回帰モデルの精度
さて、よいモデルってどういうものでしょうか?
①のグラフでいうと、それぞれの点が赤い直線に近い方がよさそうな気がしますよね。今は、けっこう近いけど完全には直線の上に載っていませんね。理論値(直線上の点)と実測値(点)にはずれが生じています。現実的には大体の場合はそうなります。あとは程度の問題です。

左の図だと、販売促進費から売上高は予測できそうですが、右の図だと、販売促進費から売上高を予測するのはあまり意味がなさそうに思えます。 (先輩から「それ、相関あるって言えんの?」と言われちゃいそうです・・)
そこで、回帰モデルの精度(理論値と実測値のずれ具合)を示す指標というものがあります。
- 重相関係数:理論値と実測値との間の相関係数です。0~1の値になります。1に近づくほど理論値と実測値が近くなって精度が高いといえます。
- 決定係数:(理論値の偏差平方和)÷(実測値の偏差平方和)です。重相関係数を二乗することでも計算できます。
ややこしくなってきましたが、回帰モデルの精度と言われたら、この辺の指標を使うんだな~とお考え下さい。(先ほどの先輩にも、決定係数を伝えて説明するとよいと思います) どちらの指標も、大きい方が精度が高いと言えます。上のグラフでは、左のほうが決定係数が大きくなります。ちなみに、説明変数を増やせば、これらの値は大きくなります。
■自由度調整
ここからは少し細かい話になります。決定係数が高い=回帰モデルの精度が高い なので、決定係数が高いことを基本的には良いことです。ただし、決定係数を高めるために説明変数を増やしすぎるのはよろしくないです。説明変数を増やすことはいわばズル行為のようなものなのです。説明が難しいですが、PCを自分流に色々カスタマイズすると、自分にとってはすごく使いやすくなりますけど、他の人が使おうとするとすごく使いにくくてダメなPCになってしまうようなものです。回帰モデルも説明変数をたくさん使ってカスタマイズしすぎると、今あるデータにはよく合う回帰モデルができるのですが、他のデータを持ってきたときに使えない回帰モデルになってしまいます。これを過学習(オーバーフィッティング)といったりします。
そこで、説明変数を増やした分だけ罰(ペナルティ)を与える自由度調整という処罰が行われます。
「キミ、決定係数、高いね。あれ?でも説明変数が多いな・・。その分、減点ね。」
こんな感じで決定係数が減点されます。減点後の決定係数を自由度調整済み決定係数といいます。状況によってはマイナスになったりします。ただし、データ数が多ければ、大きく減点はされません。すなわち、減点のされ具合は、説明変数の数と、データ数で決まります。(だから「自由度」調整という言い方をします) 共用のPCを自分勝手にあれこれカスタマイズするのはよくないですが、他の人と相談してみんなが使いやすいようなカスタマイズならばOKという感じです。
このことに関連して、いくつかの説明変数を合体して説明変数の数を少なくする主成分分析という手法もありますよ。
【H24 情報 第24問】
あるコンビニエンスストアチェーンの調査部では、各店舗の売上高を、半径1 km圏内の大学などの重要拠点数と地域人口で説明する重回帰モデルで分析している。 これに関連する記述として最も適切なものはどれか。
〔解答群〕
ア 重相関係数が負の値をとることはない。
イ 自由度調整を行っても、決定係数が負になることはない。
ウ 自由度調整を行うのは、パラメータの数に比べてデータの数が相対的に多い回帰式で、見かけ上の決定係数が高くなるからである。
エ 独立変数が2つなので、最小二乗法は使えない。
正解は(ア)です ![]()
<機械学習>
上の過去問で、「クラスター分析」という選択肢が出てきたので、機械学習についても少しだけ触れてみたいと思います。
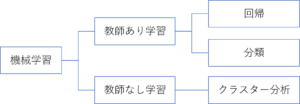
機械学習は、コンピュータにデータを読み込ませて、色々な手法(アルゴリズム)に基づいて分析させる手法のことです。大きくは、「教師あり学習」と「教師なし学習」があります。
■教師あり学習
問題と正解のセット(教師データ)を、コンピュータに学習させます。そうすると、コンピュータが答えの出し方(アルゴリズム)を学習し、問題だけを入力した時に正解を出せるようになります。上で紹介した「回帰」も教師あり学習で使われます。他にも「分類」という手法があります。これは、例えば過去の顧客に関する情報と、ある商品を購入した orしなかった のセットを学習させ、新たな顧客がその商品を購入するかどうかを予測する、というようなものです。出力結果は「購入する」「購入しない」のような”クラス”に分類されます。顧客が購入するかどうかを事前に予測することができるので、効率的に営業活動ができますね。
■教師なし学習
データの特徴や傾向を学習させて、特徴によってグループ分けできるようにします。これがクラスター分析です。グループ分けすると何がよいかというと、例えば顧客の細分化(セグメンテーション)ができ、ターゲットを絞ったマーケティングができるようになります。
[階層型クラスタリング]
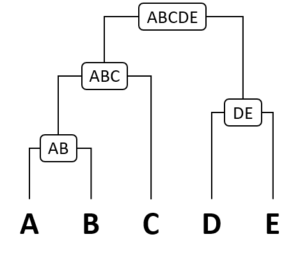
似ているもの同士を同じクラスタに、似てないものを別のクラスタにグルーピングします。トーナメント表のような図(デンドログラム)を作ります。
[非階層型クラスタリング]
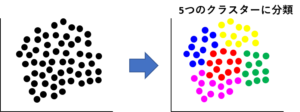
あらかじめいくつのクラスターに分けるのかを決め、決めた数の塊にサンプルを分割します。
こんな図が出てきたら、教師なし学習だな~とお考え下さい。
**********
以上、過去2回にわたり統計関連の話題を書かせていただきました。多くのデータを扱う統計学はますます重要になってくると思うので、試験でも引き続き出題される可能性があると思います。重箱の隅をつつくような論点かもしれませんが、深入りしない程度に勉強してみてください。
私は仕事でマテリアルズインフォマティクス※を少しやっているので、引き続き勉強をしています![]()
※過去の実験データ、シミュレーションデータなどを統計的に活用して材料開発を行う取り組み
![]() おまけ
おまけ![]()
経営情報システムは、ITに疎い人にとっては知らない用語や略語が多くて辛いですよね。私も以前は、職場の隣の席のおじさんが「私の頭は揮発性メモリですから・・w」なんて冗談を言ってきても、うまい返しができませんでした。 オン春でも紹介しましたが、私は、「分かりそう」で「分からない」でも「分かった」気になれるIT用語辞典 というWebサイトを参考にしていました。過去問を解いていて、珍紛漢紛な内容が出てきた時に、こちらのサイトで検索すると、IT用語をざっくり説明してくれているので便利ですよ。
経営情報システムに関しては、おべんと君の単語帳や3chの 略語リスト、CKの語呂合わせも参考にしてください!
引き続き応援しています! 以上、岩塩でした。


