【渾身】統計学について【中小企業診断士】
おはようございます。岩塩です。GWの真っ只中、学習は順調に進んでいるでしょうか??私は家にこもってつん読の消費をしております。数年前に購入した「統計学が最強の学問である」を読み、感化されたのもありまして、今日は統計学の話題を書いてみます。
統計学といえば、○○分散や○○検定など、財務会計・運営管理・経営情報システムでも登場する分野です。財務会計のポートフォリオ理論は重要論点ですが、その他の内容は「逆ザヤ沼問題」(byべりー)と認定して捨て問とする方も多いのではないでしょうか。
私は統計学をまともに勉強したことがなかったので、診断士試験では深入りしないようにしていました。というか諦めました・・・ orz 診断士試験の科目として勉強するには勉強のコスパがあまりよくないので、得意でない方は後回しにしたほうがよい分野かと思います。しかし一方で、大量のデータを扱うことがますます重要になっている昨今。今後も関連問題が継続的に出題されると予想します。そこで、統計学のイメージをざっくり理解しよう!というコンセプトで記事を書いてみたいと思います。
contents
<全体像>
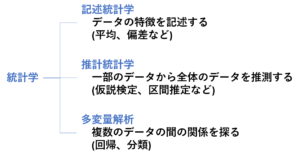
統計学はこんな感じの体系となっています。今日は、記述統計と推計統計について書いてみます。
<記述統計>
「平均」、「分散」などは、データ群の特徴を記述するものです。例えばA君とB君が11回のテストを受けました。二人とも平均点は60点でした。平均だけ見ると二人とも同じくらいの学力といえそうですが、どうでしょうか。テストの結果をヒストグラムにしてみると、以下のような結果でした。
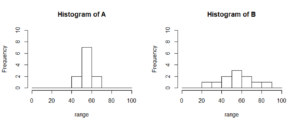
A君は70点以上の高得点は取れませんが、40点以下になることもなく、安定して点数が取れています。一方B君は波があり、80点以上の高得点を取ることもありますが、20点台になってしまうこともあります。B君の方が点数のばらつきが大きいです。ばらつきの指標である標準偏差はA君:6.9、B君:18.4で、ばらつきが大きいと標準偏差が大きくなります。ばらつきが大きいのは危険(=高リスク)です。これが診断士試験であれば、A君は合格、B君は・・・![]()
株式も同じで、大儲けはできないけど損もしない株(A君タイプ)と、大儲けできる可能性もあるけどちょっと損する可能性もある株(B君タイプ)があります。どちらも平均60点でリターンは同じですが、ばらつきの小さいA君タイプ株のほうがリスクが低いです。一方、B君タイプ株を単独で持つのはリスクが低いです。B君タイプ株が損する時に逆に儲けてくれるような株を組み合わせて持てばリスクが下がります。逆の動きをする株は、相関係数が-1に近くなるような株です。(そんな株が都合よくあればよいのですが・・・)
分散、標準偏差、共分散、相関係数の式は重要なので必ず覚えておきましょう。分散は偏差を二乗するので必ずプラスの値になります。(よって標準偏差もプラスになる) 一方で、共分散はプラスにもマイナスにもなりえます。
<推計統計>
運営管理の品質管理は重要ですが、全数検査が難しいこともありますよね。そういうときには、全ての製品(母集団)の中からいくつかを抜き取り(標本)、抜き取ったものを調べて、全ての製品のことを推定します。区間推定と仮説検定という手法があります。
- 区間推定:母集団の特徴が不明で、どの範囲にあるかを推定する
- 仮説検定:母集団の特徴がだいたいわかっていて、本当に正しいかどうか確かめる
例えば、
部品を前例がないほど長期間在庫した後、どのくらい劣化しているかを推定する場合⇒区間推定、
図面上10cmの部品を生産して、ちゃんと10cmになっているかどうかを判定する場合⇒仮説検定、
を使います。
■区間推定■
サンプリングしたものを使って、全体の傾向を「だいたいこのくらい」と推定するのが区間推定です。例えば、在庫中の部品からいくつかを抜き出して、それらの破断強度を測定します。その結果を使って区間推定をすると、例えば「部品の破断強度の平均値は、95%の確率で573~579の間にある」のような結果が得られます。部品全体の破断強度は正規分布になっているだろうと仮定して推定します。95%は信頼係数といいます。95%を使うのが一般的ですが、場合によっては90%や99%を使うこともあります。
破断強度を調べるために在庫している銅線をサンプル調査し、10個のデータを得て、平均値の区間推定を行った。以下のうちで最も適切なものはどれか。ア 自由度を10として計算する。
イ 信頼係数95%で区間を求める場合、区間は-1.96σから+1.96σの範囲である。
ウ 推定には,標準正規分布を使う。
エ 母集団分布は正規分布を仮定する。
母集団は正規分布だと仮定するので、正解は(エ)です![]() 正規分布に関しては9代目桃ちゃんの記事も参考になります。
正規分布に関しては9代目桃ちゃんの記事も参考になります。
■仮説検定■
仮説検定では、実証したい内容の仮説と、その反対の仮説という2つの仮説を用意し、反対の仮説は正しくない!と棄却して、実証したい仮説が正しいことを示す、というアプローチを取ります。実証したい内容を対立仮説、反対の仮説=帰無仮説、といいます。(ちょっとややこしいですが、用語は覚えておくといいかもしれません) 例えば、超能力があると主張したい場合は、
- 対立仮説(実証したい内容):超能力はある
- 帰無仮説(反対の内容):超能力はない
とします。

ある工場では、自動設備を利用して飲料の瓶詰を行っているが、瓶に詰められた内容量のバラツキを抑制する目的で新設備を試作した。この工場では、仮説検定を行うことで、試作機の性能向上を確かめたいと考えている。(設問 1 )
現有設備を使用したときの内容量の標準偏差σ0が1.1 ml であることから、新設備を使ったときの内容量の標準偏差をσとしたもとで、以下のように帰無仮説H0を設定した。対立仮説H1として、最も適切なものを下記の解答群から選べ。
H0:σ2=1.12
〔解答群〕
ア H1:σ2<1.12
イ H1:σ2>1.12
ウ H1:σ2=1.12
エ H1:σ2 ≠ 1.12
対立仮説=実証したい内容です。実証したいのは、バラツキすなわち標準偏差が現有設備の1.1より小さくなっていることなので、正解は(ア)です![]()
ここから少し細かい話になりますが、帰無仮説を棄却するかどうかは、実際にデータを取ってみて、その結果が帰無仮説のもとで十分に起こりにくいかどうかを確認します。
例えば、コインの裏表で勝ち負けを決めるゲームがあるとします。例の自称・超能力者がそのゲームで5回連続勝ったとします。
5回連続で勝つ確率は
(1/2)×(1/2)×(1/2)×(1/2)×(1/2)=0.03
です。これをp値と言います。これを高いとみるか低いとみるかは人それぞれになってしまうので、p値を高いとみるか低いとみるかの判断基準をあらかじめ決めておきます。この判断基準が有意水準αです。(αは0.05とか0.01とかを使うことが多いです) p値がαより小さい場合は、帰無仮説の状況下では起こりにくいことが起こったということで、帰無仮説を棄却します。
- α=0.05を使った場合、
p値(0.03)<有意水準α(0.05)
となるので、帰無仮説を棄却します。
(5回連続勝利は十分珍しい。超能力がないとは言えない) - α=0.01を使った場合、
p値(0.03)>有意水準α(0.01)
となるので、帰無仮説を棄却しません。
(5回連続勝利は十分に珍しいとは言えない。超能力がないことを否定できない)
※ちなみに帰無仮説を棄却しないということは、帰無仮説が正しいと認めるということではなく、どちらの仮説もよくわからないということになります。
ついでに下記の用語も確認しておきましょう。
第一種の過誤:帰無仮説が正しいにも関わらず、帰無仮説を棄却してしまうこと。
(上記の例でいうと、超能力はあると結論付けたが、実は超能力ではなくただの偶然だった、という場合です。有意水準αの確率で第一種の過誤が起こります。)
第二種の誤認:帰無仮説が正しくないにも関わらず、帰無仮説を棄却しないこと
(上記の例でいうと、実際は超能力はないけど、超能力がないことを否定できない状態です。αを小さく設定すると、第二種の過誤を犯す確率が上がります。)
細かい話で嫌になると思いますが、最後に検定の種類について書いておきます。データ群の内容によって、p値の計算方法が異なります。t分布を従うのがt検定、カイ二乗分布に従うのがカイ二乗検定、といった具合です。いくつかの検定について、どんな時に使うのかまとめてみました。
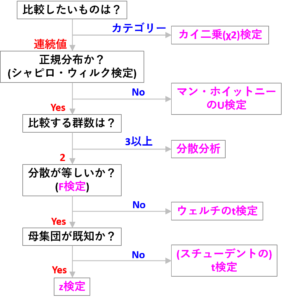
(「みんなの医療統計 12日間で基礎理論とEZRを完全マスター!」を参考に作成)
tとかzとか、呼び名の由来も規則性もよくわからなくてややこしい・・・「分散分析」という名前なのに、分散が等しいかどうかを検定するのはF検定とは・・・ など色々つっこみたくなります。
統計的仮説を検定する方法には様々なものがあり、適切に使い分ける必要がある。以下の文章の空欄A~Cに入る用語の組み合わせとして、最も適切なものを下記の解答群から選べ。母分散が未知の2つの母集団の平均の差を検定したい。2つの母集団からそれぞれ独立に、十分に大きな数の標本を採取できる場合には、標本平均は正規分布に従うと考えて、 標本の不偏分散を母分散の代わりに使って[A]を適用できる。少数の標本しか得られない場合には、母分散の信頼できる推定ができないので、[A]を使えない。しかし、2 つの母集団が共に正規分布をし分散が等しい場合には、[B]が利用できる。その場合、2つの母集団の分散が等しいことを検定するには、[C]を利用することができる。
| A | B | C | |
| ア | F検定 | t検定 | z検定 |
| イ | F検定 | z検定 | t検定 |
| ウ | t検定 | F検定 | z検定 |
| エ | z検定 | t検定 | F検定 |
Cは分散が等しいことを検定するのでF検定ですね。正解は(エ)になります![]() Aは「標本の不偏分散を母分散の代わりに使って」とのことなので、母集団が既知と捉えることができるためz検定、Bは母集団未知のためt検定です。
Aは「標本の不偏分散を母分散の代わりに使って」とのことなので、母集団が既知と捉えることができるためz検定、Bは母集団未知のためt検定です。
t分布やカイ二乗分布をもう少し知りたいという方は、ハンバーガー統計学をというWebサイトが参考になるので読んでみてください!
(ポワソンやベルヌーイなど、色々な分布についても書こうかと思いましたが、今回はやめておきます・・・)
<まとめ>
まずは財務会計のリスク&リターン、ポートフォリオを確実に理解するようにしましょう。そして、運営管理・情報システムの推計系の問題はあまり無理しないようにしましょう。
********************************
最後に告知をさせていただきます!
私も参加している受験生支援団体のタキプロがオンラインセミナーを行います!受験生のお悩み、ご質問をひとつでも多く解消するために、小グループ単位でのディスカッションをメインにした「個別よろず相談会」を計画中です。勉強方法の疑問解消に、モチベーションアップに、あるいはちょっと息抜きに・・。ぜひぜひご参加ください!道場のセミナーとはまた違った話が聞けると思いますよ。 11代目さとまる&いけちゃんも登場予定です!
![]() タキプロ春セミナー2020
タキプロ春セミナー2020![]()
(Zoomオンラインセミナーです)
日時 2020年5月17日(日)16:00開始
プログラム
第1部 個別よろず相談会 16:00~17:30
第2部 オンライン懇親会 17:30~19:00
※第2部はご希望の方のみ
参加費 無料
定員 50名
お申し込みはこちらからお願いします![]()
以上、岩塩でした(_ _)
☆☆☆☆☆☆☆
いいね!と思っていただけたら
![]()
にほんブログ村
↑ぜひ、クリック(投票)お願いします!↑



親しみにくい統計学をできる限り親しみ易く、かつ過去問解説もつけて頂きありがとうございます!
たけさん、コメントいただきありがとうございます!統計学、特に推計の問題ですが、多くの周辺知識が必要になるので、とっつきにくいですよね。関連の問題はなんだかんだ毎年出題されていますが、用語を覚えておけば解答できる問題もあったりしますので、コストパフォーマンスのよさそうなレベルで対策をしておけばよろしいかと思います!ご健闘をお祈りいたしますm(__)m