【事例Ⅳ】複利現価係数と年金現価係数をまず理解しよう！

こんにちは！まさや～ん＠5代目です

先日違うグループのセミナーでパネラーとして発表させていただきました。
６０人超えの人に喋るという機会はこれまでなかったので緊張しまくりました、でもこういう新しい経験ができるのも診断士とってよかったなぁと思いました。これからも積極的に機会をGetしていきますので応援(?)よろしくお願いします

==

今回は前回に引き続き事例Ⅳの頻出論点であるNPV関連についてです。

このテーマは
１．複利現価係数と年金現価係数
２．設備投資の経済性計算
３．デシジョンツリー
の３部作予定です。

本日のテーマは「複利現価係数と年金現価係数」です！

まず複利現価係数について

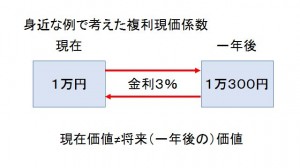
上図にあるように、利子などがあると現在価値≠将来価値となることがわかると思います。

現在の１万円は銀行などに預けることにより年３％の利子が付くとすると、一年後には１万３００円となり現在の１万円より高くなることがわかります。

将来価値＝現在価値×(1+利子率)
１万３００円＝１万円×(1+0.03)

１年後に１万３００円が必要といった場合は、将来価値を割引いて現在価値を求める必要があります。
ちなみにこの時に使う割引率が複利現価係数というわけです。

現在価値＝将来価値×複利現価係数
１万円＝１万３００円×(1/(1+0.03))

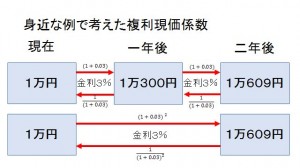
また、割引率３％で２年目の複利現価係数とは上図の下のようなイメージとなります。

現在価値＝将来価値×複利現価係数
１万円＝１万６０９円×((1/(1+0.03))×(1/(1+0.03)))

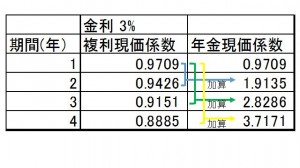
この複利現価係数をまとめていったのが複利現価係数表となります。
事例Ⅳとかでは試験に使用する一部のみ与えられてることが多いです。
※つまりは試験を解くうえでのヒントになるってことです( *´艸｀)

また、年金現価係数は複利現価係数を加算していったもので

n年目の年金現価係数＝1年目の複利現価係数＋２年目の複利現価係数＋・・・＋n年目の複利現価係数

ということです。

さて、ここまでで複利現価係数と年金現価係数をなめたことになります！
それでは実践してみましょう♪

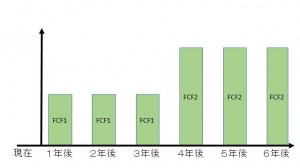
上の図はよく予備校とかで与えられるパターンですね。
これを幾つかの解法で解いていきたいと思います。

１．複利現価係数のみ与えられている場合

NPV＝FCF1×1年目の複利現価係数＋FCF1×２年目の複利現価係数＋・・・＋FCF2×６年目の複利現価係数

２．年金現価係数のみ与えられている場合

NPV＝FCF1×３年分の年金現価係数＋FCF2×３年分の年金現価係数×（３年分の年金現価係数-２年分の年金現価係数）
※３年目の複利現価係数＝３年分の年金現価係数-２年分の年金現価係数

３．６年分の年金現価係数と３年分の年金現価係数が与えられている場合

NPV＝FCF2×６年分の年金現価係数-（（FCF2-FCF1)×３年分の年金現価係数）

まとめ

複利現価係数と年金現価係数は作問者がどう解いてほしいのかという道しるべ。
与えられた場合はその意味をくみ取って計算してあげよう！
与えられない場合はなくてもできるという意味がある（H２０年事例４の問２経費部分）。

次回は、設備投資の経済性計算です。こうご期待

１．複利現価係数と年金現価係数
２．設備投資の経済性計算
３．デシジョンツリー

ではでは、まさや～んでした