【渾身】なぜ割引率から成長率を引くのか？【財務・会計】
当サイトを初めてご覧になる方へ。
当サイト「中小企業診断士試験 一発合格道場」は、中小企業診断士試験の合格を目指す方向けに、代々の合格者が勉強のコツや診断士としての活動の様子などを書き綴っています。 受験生以外の方も、中小企業診断士という存在に少しでも興味を持って頂けたら嬉しいです^^どうも、Tomatsuです。
（前回までの記事はこちら）
いつも道場ブログを読んで頂き本当にありがとうございます。
さて、突然ですが、財務・会計における理論株価の計算や企業価値計算において以下の疑問が湧いたことはありませんか？
|
① なぜ配当金を期待収益率で割ると理論株価が算出できるか ② なぜ成長率を考慮する場合、期待収益率から成長率を引くのか？ |
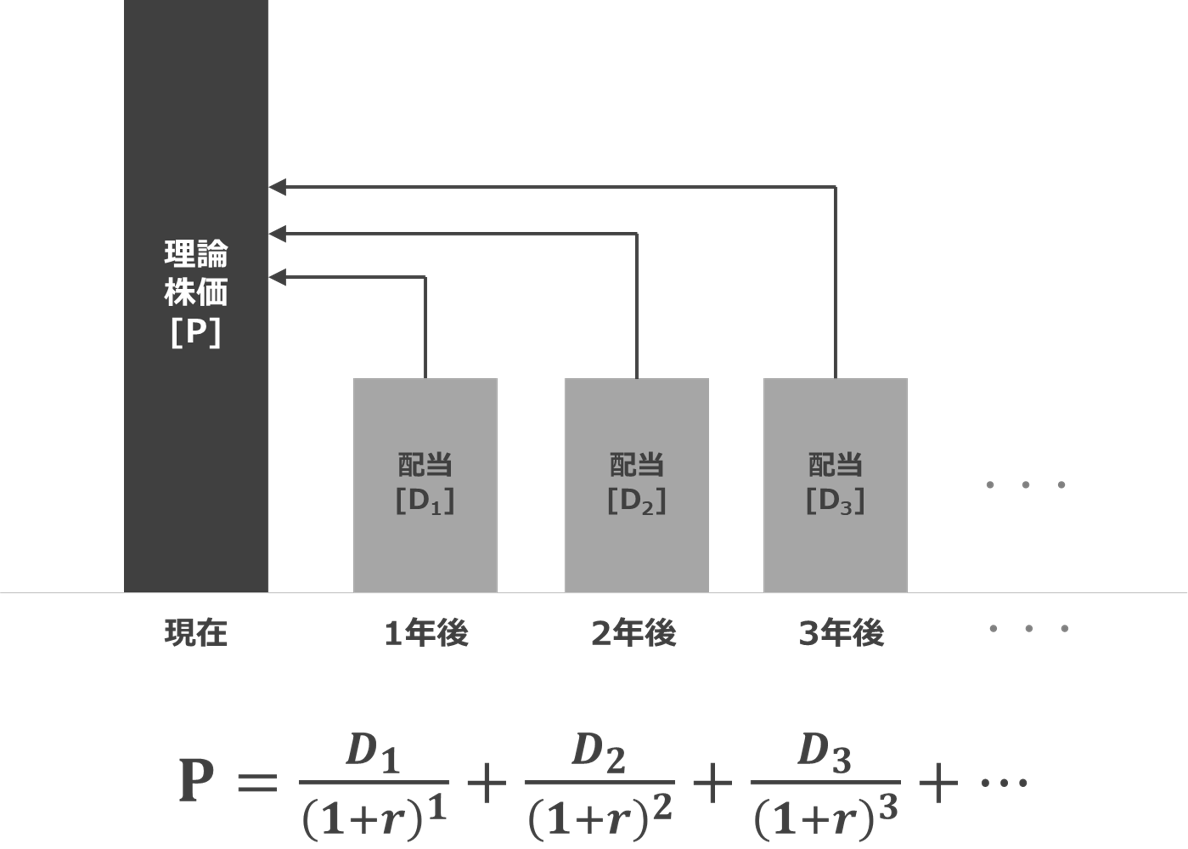
ちなみに理論株価の計算、企業の継続価値の計算式は以下の通りです。
これらの式は下記のような問題で使いますよね。
1年後の配当は105千円、その後毎年3％の成長が永続することを見込んでいる。割引率（株主資本コスト）が年5％である場合、配当割引モデルに基づく企業価値の推定値として最も適切なものはどれか。
（ア）1,575千円
（イ）2,100千円
（ウ）3,500千円
（エ）5,250千円
こういった問題は、公式さえ覚えておけば瞬殺できますよね。
なので、多くの方は単純に公式を暗記しているかと思います。
ただ、読者の方々の中には私のように「公式の意味を理解していないと気が済まないという方」もいらっしゃるのではないでしょうか？
本記事ではそういった方々向けに、上記の公式の意味と導出法をおさらいしたいと思います。
極力分かりやすい解説を心掛けておりますが「数式を見ると吐き気がする」という方は、ここでそっとブラウザを閉じて頂き、明日のべりーの記事で会いましょう。
| 【こんな人におすすめの記事】 ✅ 配当割引モデル、企業の継続価値計算の式の意味を理解したい方 ✅ 数学アレルギーのない方 |
(1) 等比数列の和の公式の考え方を使う
上記の式は全て「等比数列の和の公式」の考え方を使う事で導出できます。
高校数学を忘れた方はこんな顔になっているかもしれませんが、細かく説明していきますので辛抱下さい。
(a) 配当割引モデルにおけるゼロ成長モデル
まずはゼロ成長モデルから見ていきましょう。
配当が永続的に続くと仮定しますので、現価係数を用いて一つずつ計算していく訳にはいきませんよね？
実はこのPの式、等比数列というもので、等比数列の和の公式の考え方を適用すればもっと簡略化できるのです。
導出過程は以下の通り。
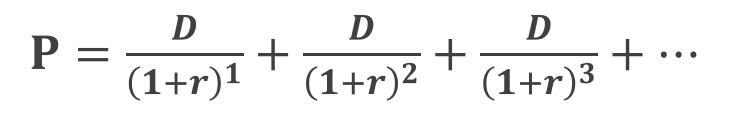
この数列における公比（各項に共通する比率）は 「 1 / ( 1 + r ) 」 であることが分かります。
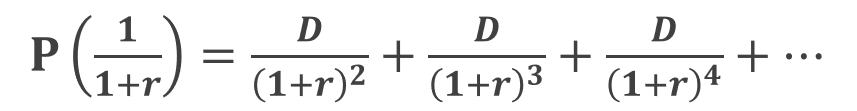
が得られます。 つぎに両式の差を取ると
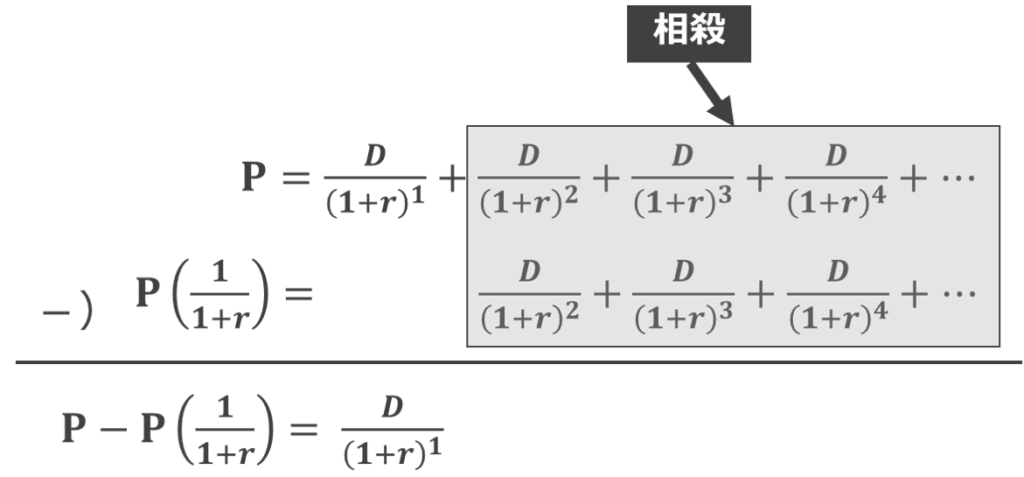
が得られます。
最後の式、めちゃくちゃシンプルで気持ち良いですね。
自分で鉛筆を動かしながら確認すると理解が深まるかと思います。
つぎに定率成長モデルがなぜ下記のような式になるのか？について見ていきましょう。
定率成長モデルは、将来得られる配当が一定の成長率で増加していくと仮定したモデルです。
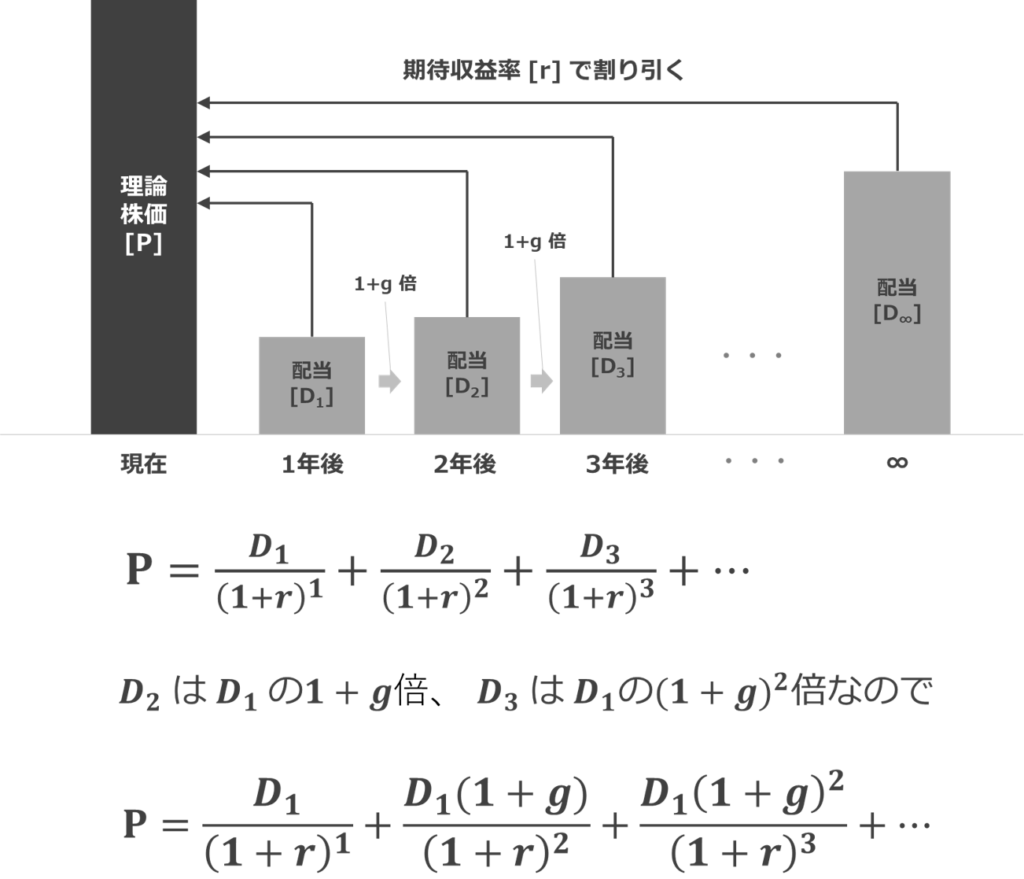
これもゼロ成長モデルの時と同様、等比数列の和の公式の考え方を使って簡易化すれば良いのです。
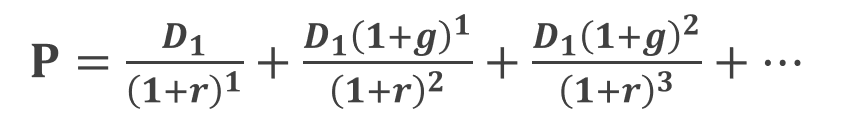
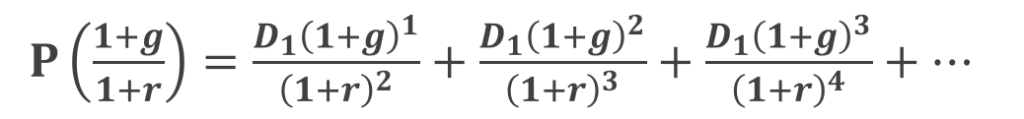
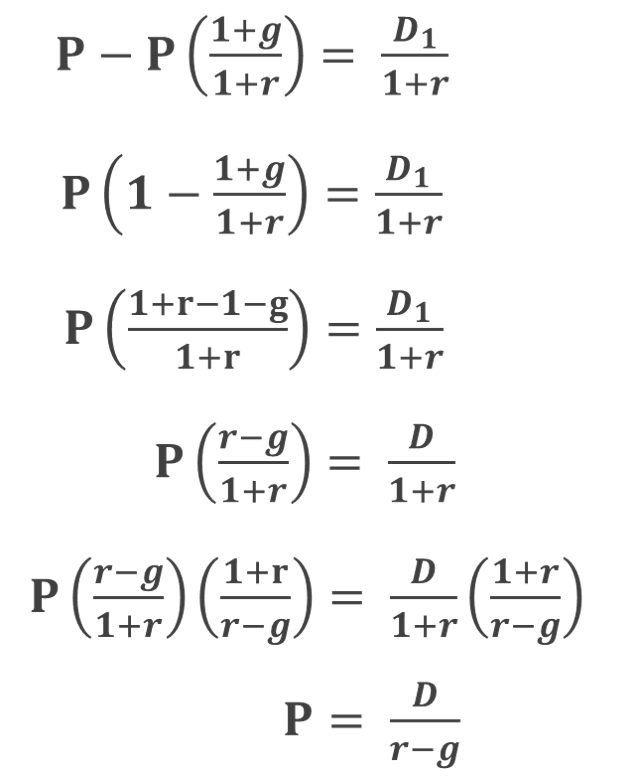
が得られます。
すっきりしましたね！
ちなみに企業価値における継続価値計算の式も全く同じ方法で導出できます。
この導出を理解しておくと、ど忘れをした際のバックアップになりますし、何より式の意味を理解して使った方がカッコ良いですよね。
ただし、問題を解く上で上記の導出を知っている必要はありませんので、余裕が無い方は公式を暗記しちゃってくださいね！
財務・会計では他にも財務レバレッジの ROE = ( 1 － t ) [ ( ROA + ( ROA － i ) × ( D / E ) ] など、導出過程が分からないと意味不明な式がたくさんあります。
万が一需要があれば、このあたりの細かい解説記事も用意したいと思いますのでコメントでお知らせください m(_ _)m
(2) おまけ：中小企業診断士川柳
今日はおまけサブカルコンテンツとして「中小企業診断士川柳」なるものを紹介したいと思います。
なんじゃそりゃ！？と思われたかもしれませんが、私も初めて知った時は同様のリアクションをしました笑
中小企業診断士川柳とは「東京都中小企業診断士協会」が主催するイベントで、平成28年度から開催されているようです。
内容は中小企業診断士から募集した川柳から入選作品を選び「中小企業診断士の日（11月4日）」を祝したイベントで表彰するというものです（最優秀１句：3万円、優秀２句：1万円）。
サラリーマン川柳の中小企業診断士バージョンみたいなもんですね笑
昨年の令和元年度は、なんと469名から1221句の応募があったようです！
で、どんな作品があるのかな？とホームページをのぞき込んでみたら力作ばかりでびっくりしました。
ここでは、個人的に良いなと思ったものを紹介させて頂きます。
（タケリオ氏：H28 最優秀賞）
・ 歯車じゃ なくエンジンに なれる場所
（さごじょう氏：H28入選作品）
・ ＡＩに 書けぬ愛ある 診断書
（ゆん卓氏：H29最優秀賞）
・ 指名請け 使命をもって 示す道
（「しめ」くくり氏：H29入選作品）
・ 「オレ継ぐよ」 うれしさ隠し 「まだ早い」
（ゆん卓氏：H30最優秀賞）
・ 「継ぐ」という 息子の猪口に 酒をつぐ
（今日氏：H30入選作品）
・ 起業本 妻が内緒で メルカリへ
（やすよ氏：R1入選作品）
・ 初受注 スマホ片手に 頭下げ
（ゆんたく氏：令R1特別賞）
（引用元：東京都中小企業診断協会HP）
それでは最後まで読んで頂きありがとうございました！
明日は神クオリティの記事に定評のあるべりーさんの登場です！お楽しみに^^
最近財務・会計の勉強を始めた者ですが質問があります。
低率成長モデルにおけるP – P(1+g)/(1+r)の計算について、
いったんn年後までの総和と考えると、右辺には
-D1(1+g)^n-1/(1+r)^n が相殺されずに残りますよね。
(1+g)/(1+r) = Rとおくと、
-D1(1+g)^n-1/(1+r)^n = -D1・R^n/(1+g)
企業が永続するとして、
lim(n→∞)R^nが0に収束していくからこの項は無視していいということなのでしょうが、
それはRの絶対値が1未満だから成り立つ話ですよね。
gもrも正の値として考えていますから、Rの分母 > Rの分子（>0）、
つまりr > g だという前提に立っていると解釈しました。
この r > g 、つまり配当金が期待収益率以上に成長することはありえない、
というのは前提とか常識の話なんでしょうか？
文字に起こすとそりゃそうか、という気もしますが、
数学的に検証する過程で引っかかったので解説いただければ幸いです。
今更ながらで大変恐縮ですが、「企業の継続価値」を求めるとき、成長率：ｇが与えられた場合、計算式の分子が「予想期間の翌期のFCF（そもそも、この意味がわかりにくいのですが）」となる計算根拠をご教示頂ければ幸いです。
ご解説にある等比級数は理解できます。
宜しくお願いします。
今年こそさん、
いつもコメント頂きありがとうございます！
そして分かりにくい表現で申し訳ございませんでした。
DCF法に基づいて企業価値を計算する問題では、下記の二種類の情報が与えられるのが通常です。
①予想されるFCF（例えば向う3年間）
②それ以降のFCF（4年目以降）
そして(2)には二パターンあり、
(a) ①の最終年度のFCFをそのまま使うパターン（ゼロ成長）と、
(b) ①の最終年度のFCFが「ある成長率」で成長することを仮定するパターン
に分けられます。
予想期間の翌期のFCFとは、①の最終年度の翌年のFCFを指します。
計算式の根拠については、下記リンクに図を交えた解説をまとめておりますので、こちらを参照頂ければ幸いです。
https://tomatsu-keiei.com/registered-management-consultant-discount-cash-flow/
よろしくお願い致します。