【運営管理】感情で覚える公式集〜商圏分析・資材発注〜 byはっしー
☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆
やっほー！はっしーです！
関東地方も梅雨入りし、ジメジメした日が続いていますね。
なんとなく気分もどんよりしがちですが、外で遊ぶのが億劫だという感情を利用して、集中して勉強してみるのもおすすめです。
今回は、感情と紐づけて運営管理のちょっと覚えづらい公式を覚えてしまおうという企画です。
はじめに
１次試験の運営管理ではいろいろな公式が出てきます。
勉強を始めた当初の文系受験生の私は…
うーん…捨てたわ！！！
となかば覚えるのを諦めていました。
しかし、勉強を進めていくうちに気がついたことがあります。
これらの公式は実際の事例を計算式の形で表したものであり、バックグラウンドのストーリーを想定することで暗記できるのではないかということです。
ということで、今回は文系受験生の戦略として、運営管理で出題実績のある「ライリーの法則」と「経済的発注量」の公式を感情を意識して覚える方法をご紹介します。
計算式の暗記に不安がある方も、今回の記事が数式の意味を読み解く癖をつけるきっかけになれば幸いです。
※ご注意
今回の記事で紹介するバックグラウンドは、公式を覚えるために独自に想定したものです。
診断士試験での出題実績はほとんどありませんが、それぞれ学術的な考え方は別にあります。
あくまで基本的な考え方の導入と公式の暗記のためにご活用いただきますようお願いいたします。
それでは始めて行きましょう！
基本的な考え方
まず前提条件として知識として覚えてもらいたいことが一つあります。(簡単な算数レベルなので安心してください)
分数は「分子が増加→大きくなる」「分母が増加→小さくなる」ということです。
ここは、先日のさたっち
の記事を読んでいただいた方はバッチリではないでしょうか。
不安のある方は、経済学向けの内容ですが、数学の基礎知識がわかりやすくまとめられていますのでぜひご参照ください。
では分母の中にさらに分数があるパターンはどうでしょう？
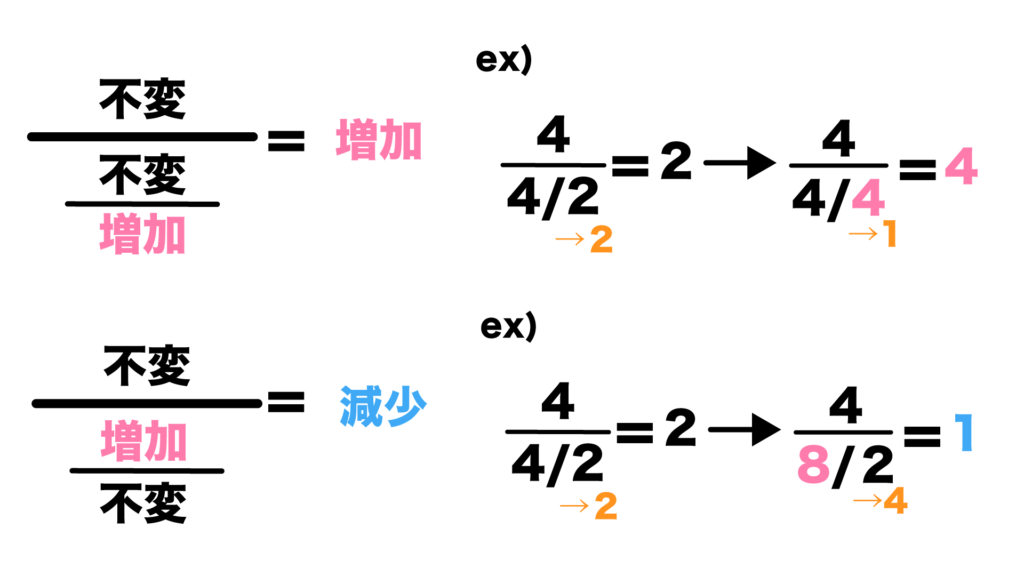
分母の中の分数は「分母が増加→大きくなる」、「分子が増加→小さくなる」ことがわかります。
運営管理で登場する公式ではよく出でくるパターンなので、この前提を覚えておくだけで公式が頭に入りやすくなると思います！
感情で覚える計算式 〜商圏分析編〜
それでは、さっそく実際に数式を見ていきましょう。
まずは商圏分析より「ライリーの法則」と「ライリー＆コンバースの法則」です。
ライリーの法則
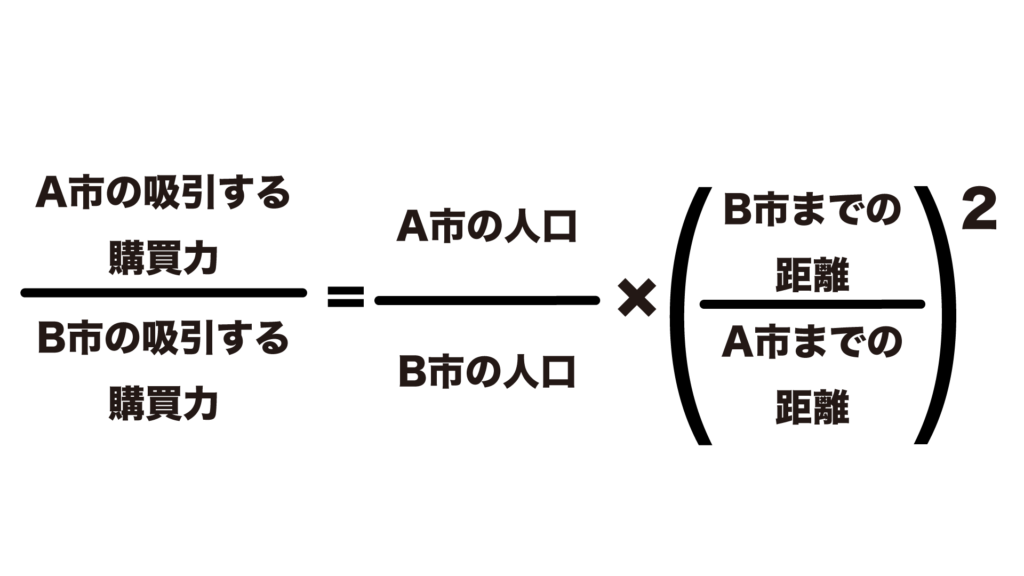
ライリーの法則の公式では、2つの都市の吸引する購買力の比率を表しています。
分子はA市の吸引する購買力、分母はB市の吸引する購買力です。
つまり分子が大きい方が、中間の都市の住民にとってA市はB市よりも買い物に行こうと思われやすいということです。
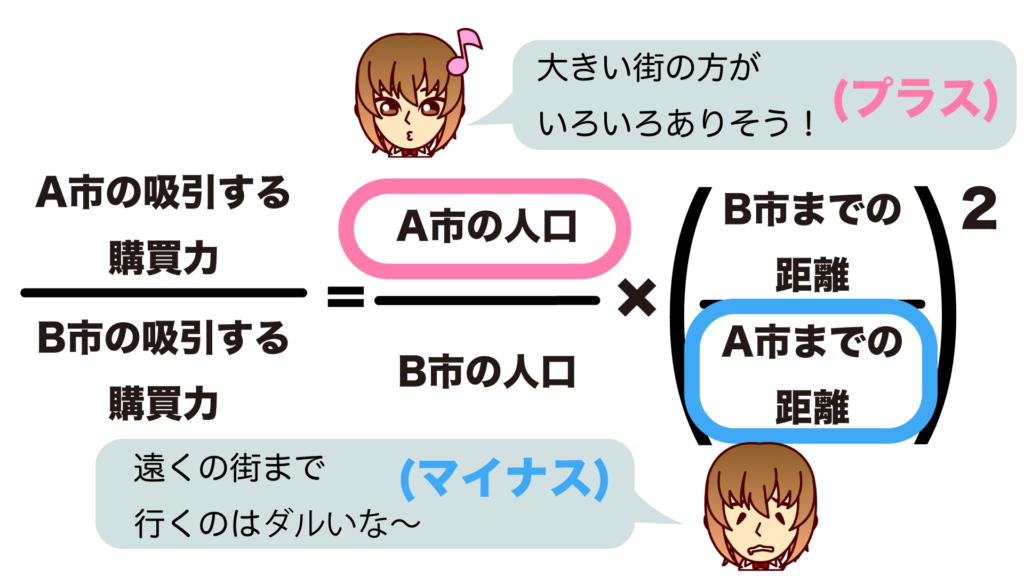
吸引力を決めるのは中間の都市に住む消費者のこの二つの感情です。
お店の数も多そうだし大きい街に行きたいな〜
この感情は、A市の吸引する購買力(A市の魅力)にはプラスに作用します。
つまり「A市の人口が多い→分子(A市の吸引する購買力)を大きくする→分子にA市の人口」がくるということです。
次に、後半部分が表している感情を見ていきましょう。
大きい街でも遠かったらわざわざ出かけるのはしんどいな〜
この感情は、A市の吸引する購買力(A市の魅力)にはマイナスに作用します。
こちらでは「A市までの距離が大きい(A市まで遠い)→分子(A市の吸引する購買力)を小さくする→分母にA市までの距離」ということになります。
図解するとこのようになります。
ちなみに、なぜ距離の方を二乗しているのは、距離は人口よりも重要な要素であるため比重を重くするためです。
ライリー＆コンバースの法則
ライリー＆コンバースの法則の公式は次の通りです。
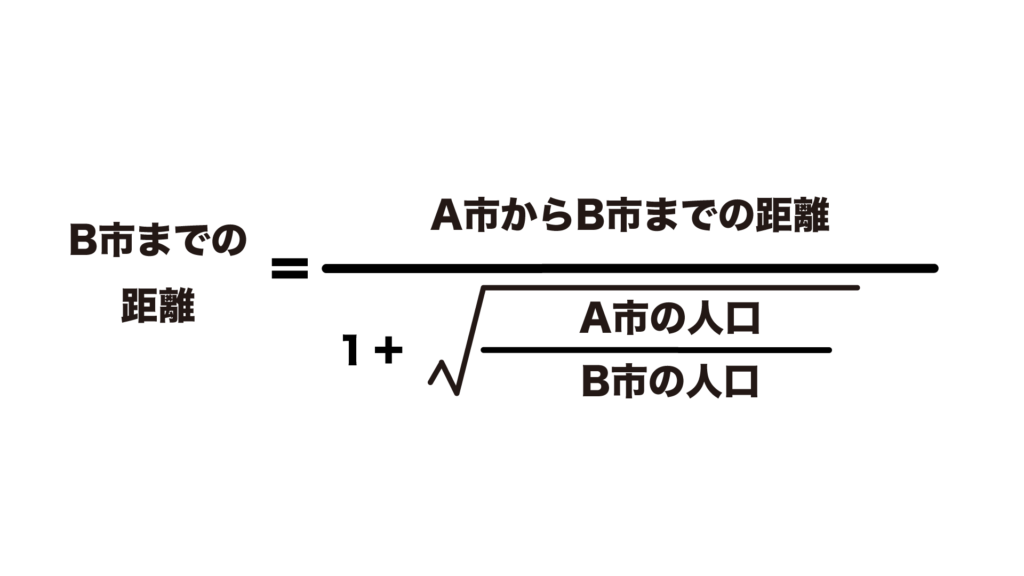
ライリー＆コンバースの法則では、２つの都市の商圏の分岐点を表しています。
この状況を図解するとこのようになります。
まずはB市までの距離が大きい状況です。
このパターンでは、商圏分岐点はA市に近くなりA市の吸引する購買力が弱いことを表します。
では、逆にB市までの距離が小さい状況ではどうでしょうか。
このパターンでは、商圏分岐点はB市寄りになりA市はより広い範囲の顧客を引き寄せます。
つまり、A市の吸引する購買力が強いということになります。
この前提で先ほどの式を見ていきましょう。
今回はB市までの距離が小さい方がA市の魅力が高いということですので、A市へのプラスの感情はマイナスに作用します。
つまり、先ほどはプラスに作用していた「大きい街の方がいい！」という感情はマイナス要素になります。
そのため、A市の人口という要素は分母の中の分子にきます。
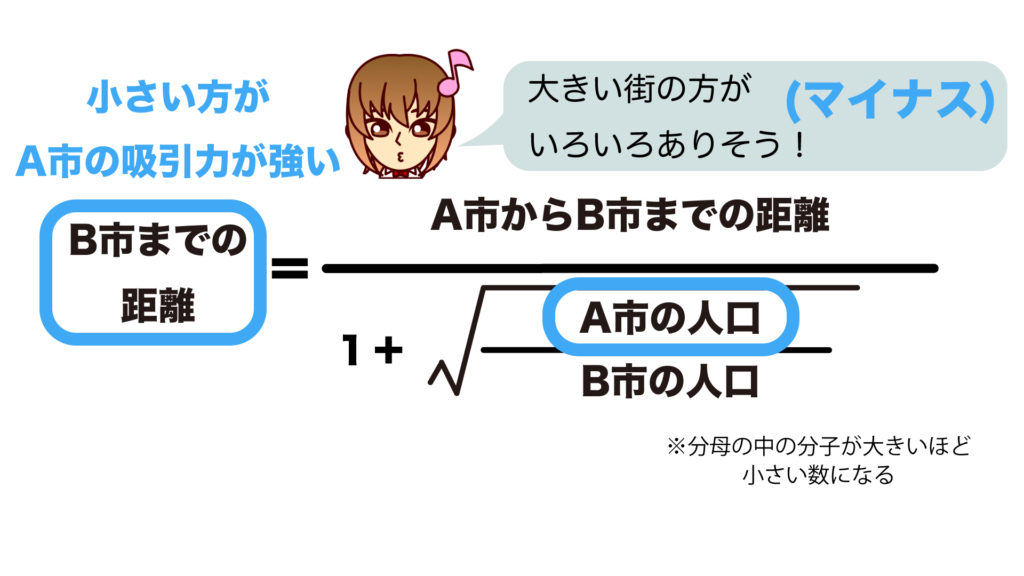
こちらも数値以外に1+√の要素がありますが、ライリー＆コンバースの法則の式はライリーの法則の式を変形させたものであるため、二乗の要素がルートの形で反映されています。
感情で覚える計算式 〜経済的発注量〜
次は、資材・在庫管理より「経済的発注量」についてです。
こちらは工場での資材発注に関する数式なので、生産現場に馴染みのない方はとっつきづらいかもしれません。
ここでは、少し解釈を変えて身近に自分が買い物をするつもりで見ていきましょう。
ということでこちらのパートでは、買い物上手なあの方にゲストとしてご登場していただきます！
呼んだ？
経済的発注量
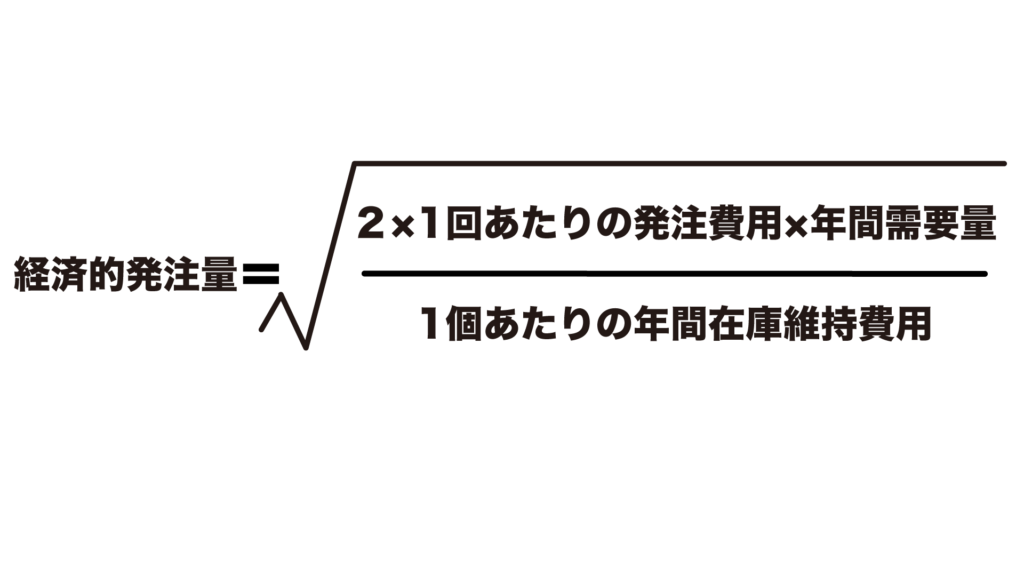
経済的発注量の公式では、年間の在庫費用が最小になる発注量を求めます。
この時の感情をそれぞれ表すとこのようになります。
送料も梱包料もバカにならんし、まとめ買いが買い物の基本や！
つまり「１回あたりの発注費用が高い→1回の発注量を増やして発注回数を減らした方がいい→発注費用は分子」ということになります。
買うたモンをウチに置いとくんもスペースが必要やし、保管費用は節約したいわ〜
こちらでは「在庫維持費用が高い→1回の発注量は少なくして在庫量を減らした方がいい→在庫維持費用は分母」ということです。
とは言うても、必要なモンはちゃんと買わんとね！
「必要な数量が多い→1回ごとに発注する量も増やす必要がある→年間需要量は分子」ということになります。
これを図表に表すとこのようになります。
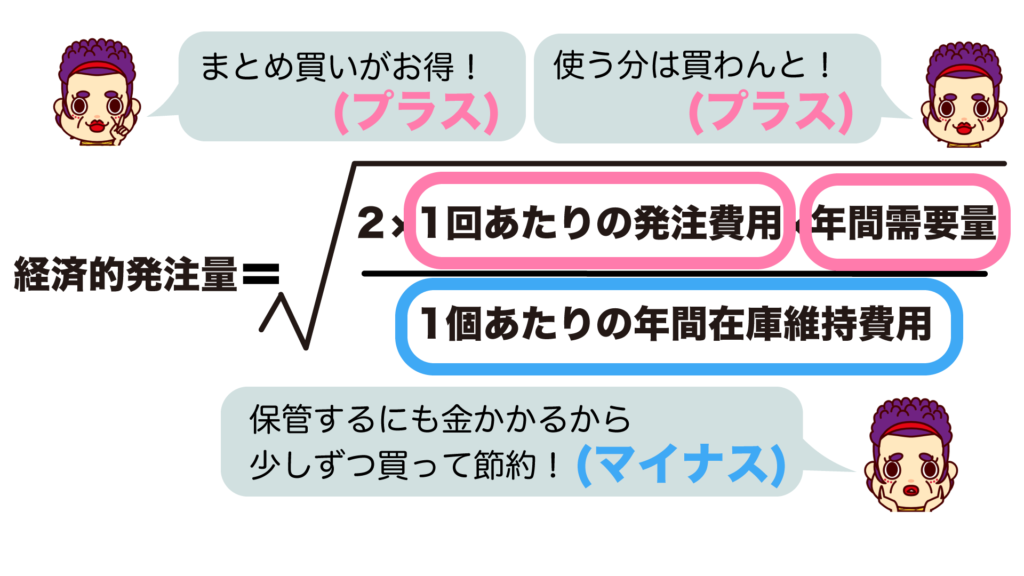
おばちゃんのおかげで数値の意味はわかったけど２とルートが謎のままだ…
今回の趣旨からは少しずれますが、ここを理解するには経済的発注量の趣旨について知る必要があります。
こちらが経済的発注量を表したグラフになります。
発注量を増やすと在庫の維持費用が増え、発注量を減らすと発注回数が増えて発注費用が増えてしまいます。
つまり、トレードオフの関係になっている2つの費用の交点で総費用が最小になり、この発注量が経済的発注量になります。
この関係を式で表すと下記の通りになり、変形すると先ほどの経済的発注量の式になります。
(平均在庫の数字”２”と、発注量が2回出てきているため二乗関数になるので変形するとルートが出現します。)
終わりに
最後までお読みいただきありがとうございます！
感情で覚える商圏分析と経済的発注量の公式はいかがでしたでしょうか。
文系受験生にとっては特に、ただの数字の羅列として覚えるのは苦痛ですが、なぜそういう公式になるのかの文脈を理解すると暗記のきっかけになると思います。
実は、店舗運営についても解説もするつもりだったのですが、初代ハカセさんの記事がこの上なく明快で私の出る幕はなさそうでしたので記事の紹介をさせていただきます。
公式を覚えれば解ける問題は、試験ギリギリまで粘れば得点源にできる分野です。
今回の記事が、１次試験に向けて公式を覚えていくモチベーションを上げるきっかけになれば幸いです。
明日はひろしです！
診断士を目指そうと思った感情を思い起こさせてくれる企画を用意しているみたいですよ！
お楽しみに！
☆☆☆☆☆
いいね！と思っていただけたらぜひ投票（クリック）をお願いします！
ブログを読んでいるみなさんが合格しますように。
にほんブログ村
にほんブログ村のランキングに参加しています。
（クリックしても個人が特定されることはありません）
