【渾身】正規分布・分散・標準偏差（情シス・財務）統計　（桃ちゃん）

おはようございます、桃ちゃんです！

先週の春セミナー、
ご参加いただいた方ありがとうございました。

また、今回ご参加いただけなかった方、次回の夏セミナーで
お会いできるのを楽しみにしています！(^_-)-☆

 

春セミナーの内容は、ヒロちゃんが、
セミナーからの関連話はzenzen、ゆう、へんりー、たかじんが
書いた記事をご参照ください。

 

さて、春セミナーで桃ちゃんは
二次試験対策として試験委員の著書をご紹介しました。

 

他にも読書本の紹介希望があったので、
前回はVE（後半）を書きます！と言っていましたが
今回は最近読んだ（実はまだ読み途中の（汗））おススメ本を
先にご紹介します！　　　VEはまた今度書きます！

 

---

「文系でもわかるビジネス統計入門」
内田学　兼子良久　斎藤嘉一　共著　東洋経済新聞社

 

なぜ、これを読もうかと思ったかと言いますと、
この４月からMBAに通っているのですが
「統計学」の先生がおススメされていたからです。

 

正直、文系出身なので
統計学は敷居が高めでした。

 

でも、この本では、難しい数式が分からなくても
統計で何ができるかが分かりやすく解説されています。

 

情報システムの統計問題と合わせながら
その本の内容で書かれているエッセンスをご紹介します。

 

■平成 ２３年度　第 ２４ 問　問題と選択肢（ウ）

「さっぱり、何のこっちゃ！」ですよね～。

 

もちろん、情報システムの統計問題は
最初から捨てる！という選択をするのもありだと思います。

 

ご自身であまりにも細かく調べる必要はないと思いますが、
このブログを通して、「まったくわかんないんですけど！（怒）」から
「あ、なるほどね～ｗ」くらいになってもらえると嬉しいかなと思います。

 

まず問題文の意味は

銅線の在庫がた～くさんあるけど、全部は数えられないから
無作為に１０個抽出してサンプル調査をしました。

でもあくまでも１０個なので、この平均が在庫全部（母集団：例えば１０万本）の
平均と一致するかはわかりません。

だから、【区間推定】一定の区間＝幅を持たせて推定するというものです。
平均値がピタッと同じ数字にはならないけど、ある程度の区間の中で推定しよう、です。

 

（イ）は、その推定に「標準正規分布」を使いますか！？という問いです。

 

これを考える前に、

 

「文系でもわかるビジネス統計入門」で書かれている
「難しく聞こえる用語」をわかりやすく“変換”することをご説明します！
「　」＝「　」は本から引用　※は桃ちゃん作成（本と関係ないです）

 

※例えば、クラス４０人の数学のテストが返ってきたとします。

 

●偏差と平均の違い

平均

０点の人が２０人、１００点の人が２０人　これは　平均５０点
５０点の人が４０人　　　　　　　　　　　これも　平均５０点

同じ平均でも意味が違いますよね。

もしこれが、売上だったら….。
売上ゼロの日もあれば、１００万の日もあるけど、
平均５０万あるから結果オーライ！ではないですよね。

そんな時は、平均からどのくらい離れている・バラツキがあるかを
調べることが重要です。

 

偏差　

平均からいくら離れているか、です。
６０点の人は平均５４点より　（６０－５４）＝＋６点　　６点＋に離れている
５０点の人は平均５４点より　（５０－５４）＝－４点　　４点－に離れている

 

この「平均からどのくらい離れているかの数値」を４０人分足すと、
６＋（－４）＋・・・＝０　　結果はゼロになります。
なので、結果を二乗して離れ具合の値を「正の数」にしたのが、偏差²です。

 

二乗すると「－×－＝＋」「＋×＋＝＋」だから正の数になります。

 

「偏差²」の合計＝６²＋（－４）²＋・・・・＝６,８４０（仮）

 

そして、その「偏差²」の合計を「データ数」（４０人）で割って
「偏差²の平均」を出したのが、「分散」です。

 

分散＝　「偏差²」合計６,８４０÷「データ数」（４０人）＝１７１

 

このままだと、二乗しているので単位が「点数²」になってしまいます。
ですので、分散の平方根をとって「標準偏差」をだします。

 

標準偏差＝√分散＝√１７１＝１３．０７・・≒１３点

 

つまり、平均の５４点からプラスマイナス１３点である人
（４１～６７点）の人が多いということです。

 

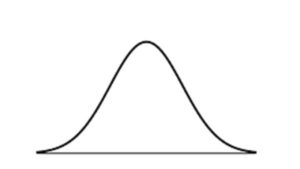
次に、正規分布についてです。

点数の「ヒストグラム」＝「グラフ」を作成すると
「平均」を中心に左右対称の曲線を描くといわれています。

これが「正規分布曲線」です。
・平均を中心とした、左右対称の釣り鐘型が特徴です。

 

「標準正規分布」とは　

　平均がゼロ、　標準偏差が１の　正規分布の事を言います。

でも、こんな事ってないですよね？
完璧に平均がゼロには滅多にならないので、統計学上の概念的な世界です。

（テストの点数は０点以上なので、全員０点出ない限り平均はプラスの数値になります）

 

今回も、銅線サンプル１０本の平均は正の値になるので
「標準正規分布」ではなく、「正規分布」などを使うことになります。

よって（イ）の答えは×バツです。

 

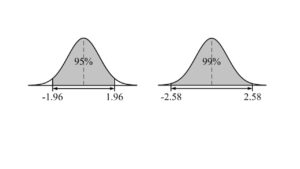
ちなみに、「正規分布曲線」には「平均」と「標準偏差」の間に、
以下の関係があると言われています。
（出典：「文系でもわかるビジネス統計入門」P２６～P２９）

 

平均を挟んで±１．９６×標準偏差の間に全データの約９５％が含まれる

平均を挟んで±２．５８×標準偏差の間に全データの約９９％が含まれる

テストの点数だと　５４±１.９６×１３点の間に約９５％が含まれる。
つまり２８．５２点から７９．４８点の間に約９５％がいるということになります。

 

 

一気に書いてきましたが、一読しただけでは
分かったような、分からないような…でしょうか。

 

桃ちゃんも、まだ本全部を読み切っていないので、
また追加の情報があればアップします！

（ただし、今の時期深追いはしないほうが良いと思います～）

 

以上、桃ちゃんでした！