【経済学】 5.ミクロ経済学知識問題
こんにちは、 Xレイ です。
今日は、ミクロ経済学の知識問題です。
といっても、ミクロ経済学からの出題の多くはグラフ問題。
特にここ3年は、その比率80%。
その他頻出領域としては、『市場の失敗』の知識問題、『ゲーム理論』
といったところでしょうか。
そこで、前半はグラフ対策でできなかった『生産者行動の理論』の領域を、
後半に、その『市場の失敗』の知識問題と『ゲーム理論』をみてみます。
過去の出題では、これらいずれの領域においても、易しい設問が多いという印象です。以下の内容も知識の確認程度です。
生産者行動の理論
1.生産関数
2.費用関数と収入関数
グラフ問題として、この領域からの出題は特徴的です。
というのは過去8年で3回、すべて上2つを同年度にそろえての出題です。
互いに関連深いのでそうしてるのか、それとも偶然か。
いずれにしても、過去の出題を見る限りそれほど難しくはないので、受験生としては歓迎でした。でも、昨年にその出題があったので、今年は・・・
1.生産関数
【出題~H26問13 H24問18 H21問13】
過去の出題では、およそ以下の事項で選択肢が構成されています。
①限界生産力逓減・一定・逓増
②平均生産物と限界生産物
まずは①。

平成24年問18で、一文だけ『規模に関する収穫逓増』としてますが、
1生産要素の場合は『限界生産力逓増=収穫逓増』として問題ありません。
そして、試験にグラフ問題として出題されるのは、1生産要素のみを考えた限界生産力逓減の生産関数になるはずです。
次に②。
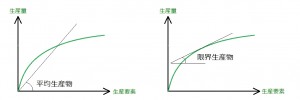
平均生産物=原点を通る直線の傾き
限界生産物=接線の傾き
過去に設問で問われたのは、この程度です。
いずれも、グラフで視覚的に捉えておければ十分だったはずです。
生産関数とは、『生産要素の投入量』と『生産量』の関係を表しています。
よってそこから、生産者が目指す生産量(=利潤を最大にする生産量)に対して必要な生産要素の投入量(=生産要素需要)を知ることができます。
そこで、その生産要素を労働力のみとしたとき『実質賃金』と『労働需要』の関係はどうなるか・・・
と、ここまで話が進むと正答率が下がって、平成26年問13の設問2。
・利潤最大化条件: 労働の限界生産性=実質賃金
・労働需要曲線は右下がり
労働市場ですが、この辺りは苦手な方が多いようです。
2.総費用曲線・総収入曲線
【出題~H26問18 H24問19 H21問13】
完全競争市場下での、総費用関数・総収入関数の出題です。
2つの関数を同時に示しての出題で、利潤や利潤最大化条件について問われます。平成24年問19をきちんと解ければ問題ないはずです。
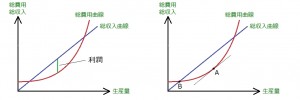
①利潤=総収入-総費用(図左)
②利潤最大化条件: 限界収入=限界費用 となる生産量(図右の点A)
①は、見ての通り。
②は、限界収入=価格=総収入曲線の傾き
限界費用=総費用曲線の接線の傾き
間違えやすそうな選択肢をつくるとすれば
図右で 〔点Bは損益分岐点である〕→×
こんな感じでしょうか。
『市場の失敗』の知識問題
【出題~H24問22 H23問15 H21問14 H20問11,15】
公共財・逆選択・モラルハザード
『市場の失敗』の知識問題といっても、これら用語がどういったものか問われる程度です。
ちなみに、平成21年問14のサーチコストの問題もこの関連なのでしょうが、もう一度出題される確率は低そうです。面白そうな話ではありますが。
ゲーム理論
【出題~H26問22 H25問21 H24問23 H23問23 H22問11,14 H22問17 H19問15】
このところ、毎年何らかの形で出題されています。
『用語の意味』を問われている、といった印象です。
そこで、頻出の囚人のジレンマ型ゲームを確認しながら、
一通り用語の整理をしておきます。
・価格引下げ競争
| Y社 | |||
| 維持 | 引き下げ | ||
| X社 | 維持 | (6・6) | (1・9) |
| 引き下げ | (9・1) | (3・3) | |
いま、X社とY社は同じ商品を同じ価格で販売し、今期の利得(利潤)は互いに6となりました。
両社は来期に向けての価格設定を、『維持』・『引き下げ』の2通りから選択をします。
【共に、来期の自社の利得ができるだけ大きくなることを目的とし、話し合うことはなく、他者の選択を知ることもできない】
いわゆる、戦略型ゲーム(非協力ゲーム)で、上はその利得行列です。
ゲームを構成する基本要素
・プレイヤー・・・X社、Y社
・戦略・・・維持、引き下げ
・利得・・・表中の数字(左がX社、右がY社)
それでは、X社・Y社それぞれの立場に立って
【相手の戦略を固定したとき、最も利得を大きくする自らの戦略】
すなわち、最適反応をみていきます。
まずは、X社。
①Y社の戦略を『維持』に固定したとき
X社の利得は、戦略を『維持』としたとき6、『引き下げ』としたとき9
このときのX社の最適反応は、『引き下げ』です。
②Y社の戦略を『引き下げ』に固定したとき
X社の利得は、戦略を『維持』としたとき1、『引き下げ』としたとき3
このときもX社の最適反応は、『引き下げ』です。
次に、Y社。こちらも全く同様に
③X社の戦略を『維持』に固定したときは、『引き下げ』
④X社の戦略を『引き下げ』に固定したときも、『引き下げ』
がY社の最適反応となることが確認できます。
ここで②と④から、X社とY社が共に『引き下げ』を選択したとき、
それぞれ相手の戦略の下で最適反応となっていることが分かります。
この【互いに最適反応となっている戦略の組合せ】がナッシュ均衡です。
ちなみにナッシュ均衡は1種とは限りません。条件によっては複数の場合もありえます。
また①と②から、Y社がどちらの戦略をとっても、X社の最適反応は
『引き下げ』ということが分かります。このように
【相手の戦略に関わらず、常に最適反応となる戦略】が支配戦略です。
同様に③と④から、Y社も『引き下げ』が支配戦略となっています。
つまり『引き下げ』『引き下げ』の組合せは、支配戦略同士でもあります。
この【互いに支配戦略となっている組合せ】が支配戦略均衡です。
支配戦略均衡はナッシュ均衡の特殊なケースであり、
プレイヤーが2人の場合、それが唯一のナッシュ均衡となります。
(1)1回限りのゲーム
これが1回限りのゲームのとき、上でみてきたように、それぞれ自社の利得を大きくしようとした結果、両社の戦略は唯一のナッシュ均衡に決まり、利得3ずつを得ます。
しかしここで、両社とも『維持』を選択すると共に利得6となって、互いに、そして全体としても利得が大きくなることが分かります。
つまり、共に最適反応をとった結果、
【互いにもっと良い状態があるのに、それよりも悪い状態に陥っている】
ということです。これが囚人のジレンマです。
このように囚人のジレンマ型ゲームの解は、
【全体として最適な状態】すなわちパレート最適な状態にはなりません。
(2)有限回数繰り返しゲーム
今度は、1回限りではありません。
2回でも、100回でもいいのですが、有限回数繰り返します。
1回限りとの違いは、将来の利益を考慮して行動できるというところです。
『1回目に自分が『引き下げ』を選択し、たまたま相手が『維持』だったら大きな利得を得る。でも、そうなると次回は間違いなく相手は『引き下げ』を選択をしてくるだろう・・・ それならば、1回目に『維持』を選択しておいたほうが良いのかも・・・』
例えばこのような感じです。
焦点は、互いに協調し『維持』を選択できるか、というところです。
結論から言うと、すべての回で『引き下げ』を選択してしまいます。
2回でも100回でも、です。
簡単に説明すると、まずは最終回に着目をします。
最終回では、次回はないので、将来の利益を考慮する必要がありません。
すなわち、そこは1回限りのゲームと同様です。
ならば、(1)でみたように互いに『引き下げ』を選択します。
すると、その前の回。
次の最終回では、相手が『引き下げ』を選択することが分かっているので、その将来を考慮する必要がなくなります。
そこで、これまた互いに『引き下げ』を選択します。
さらに前々回では、最終回とその前の回を考慮する必要が・・・
と初回まで続いて、すべての回で『引き下げ』を選択します。
理論上ではこうなるとのことです。
(3)無限回数繰り返しゲーム
さて、その最終回が無くなったらどうでしょう。
結論は、互いに『維持』を選択するという可能性が生まれます。つまり
【無限回数繰り返しの囚人のジレンマゲームにおいては、互いに協調するという解が成立する】ということです。これがフォークの定理です。
なぜそうなるかは、フォークの定理なので・・・
それではこの場合、どのような戦略が考えられるのでしょうか。
もし試験に出るとしたら、というものを2つだけ。(私見です)
①トリガー戦略
初回は『維持』を選択する。
初回に相手も『維持』を選択したならば、次回も『維持』を選択する。
そのうち相手が1度でも『引き下げ』を選択したときには、それ以降はすべて『引き下げ』とする。
②しっぺ返し戦略(オウム返し戦略)
初回は『維持』を選択する。
2回目以降は、直前回の相手の戦略と同じものとする。
最後に平成26年問22の選択肢で『割引因子の値が~』となってますが
これは財務会計でもよく出てくる現在価値の概念です。
『割引因子の値が十分に1に近い』=『ほとんど割り引かない』
これがフォークの定理に必要な条件です。
将来の利益を考慮することが重要なので、この値が小さいと別のゲームになってしまいます。
そのため、『繰り返しゲームが続く確率』と捉えることもあるようです。
今回は、以上です。
それでは、また。 Xレイ