【経済学】　労働市場（雇用の理論）

 

こんにちは、　Ｘレイ　です。

今回は、マクロ経済学の労働市場です。

まだ経済学を学習されていないというストレート生の方。
今読んでも、さっぱり解らないと思います。
いずれ学習された際、お役に立てるものとなっていればいいのですが。

「来年こそは」と励まれている方。
ここは苦手という方が多いのではないでしょうか。
おそらく、ほとんどの中小企業診断士テキストでそれほど丁寧に扱っていない上、少々解りづらいところでもあるのでしょう。
しかし近年、この領域に関連した出題が続いていますので、確実に60点をと思うなら、おさえておくに越したことはありません。
(H25問5　H26問13設問2　H27問7設問1,2　問8)

 

さて、労働市場、つまり雇用の理論をみていくのですが

古典派の労働需要に対する考え方は『古典派の第一公準』
古典派の労働供給に対する考え方は『古典派の第二公準』

と呼ばれます。（公準とは、決まりごとみたいなものです）

それら公準とはどのようなものなのかをまずはみて、そのように呼んだ経済学者ケインズは、結果一方を否定するのですが、終盤その辺りにも触れてみます。

 

古典派の労働需要

労働需要、すなわち“企業がどれくらいの労働量を必要としているか”ということです。

企業が利潤最大化行動をとる結果、『古典派の第一公準』を満たすように労働需要は決まるというのですが、その公準というのが以下。

『実質賃金は労働の限界生産物に等しい』

 

まずは、実質賃金や労働の限界生産物とは何なのかをみていきましょう。

実質賃金とは、“モノ”の単位で表した賃金です。
実際に貨幣で受け取る賃金は、名目賃金（貨幣賃金）と呼ばれます。
ここでは、その企業が生産している“モノ”で実質賃金を表します。

例えば、1個10000円の時計を生産している企業があります。
そこで働く労働者の給料を30万円とすると、

・名目賃金は　30万円
・実質賃金は　30個　　となります。

 

労働の限界生産物とは、
“労働量が1単位増加したときに増える生産物の量”です。

例えば、先ほどの時計企業に労働者が10人居たとします。
“それを11人に増員したとき、新たに何個生産量が増えるのか”ということです。

仮に、10人→11人に労働者が増えたとき、
新たに50個生産量が増えるとします。
これは、“労働者10人のときの限界生産物は50個”ということです。

限界生産物についてもう少し考えてみます。

今度は、労働者があらかじめ60人も居て、
60人→61人　に増えたときはどうでしょう。

通常は、最初の　10人→11人　のときよりも
限界生産物は少なくなると考えられます。

10人→11人　のときは50個でしたが、
例えばそれが10個になってしまうということです。

イメージするならば、使える機械の数や能力にも限りがあります。
労働者が10人のときは、半分程度の機械しか使えていなかったとすると、11人目の加入は非常に大きなものでしょう。
しかし、60人ともなると機械もフルに活用できていて、そこから1人の増員でどれほどの生産量が増えるでしょうか。

このように、一般的には、労働者数（生産要素）が増えていくほど、その限界生産物は減っていきます。
これを、限界生産力逓減の法則といいます。

ちなみに、その法則を満たす生産関数（1生産要素）を図示すると

図１

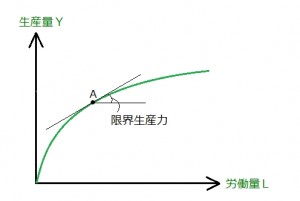
グラフにおいて、限界生産力（物）は接線の傾きで表されます。
それが逓減していく（右に行くほど小さくなる）ということは、
$Y=\sqrt{L}$　のような形状のグラフとなります。

 

余談ですが、中小企業診断士試験に出てくる生産関数は、このように限界生産力（物）の逓減しているものがほとんどです。
平成24年問18　平成26年問13　平成27年問16　で実際にそのことを問われましたが、すべて逓減です。
例外があるとすれば、経済成長論の内生的成長モデル（ＡＫモデル）。
この理論では、マクロの生産関数ですが、その資本の限界生産力を一定と仮定しています。このモデルが出題されたときには、その“限界生産力一定の仮定”と、それによって“技術進歩がなくても永続的に成長することを示せる”というところを、まずは問われるのではないでしょうか。

 

話を戻しまして、ここまで実質賃金と労働の限界生産物についてでした。

ここで再び第一公準。『実質賃金が労働の限界生産物に等しい』とき企業の利益が最大となる。よって、そのように労働者を雇用する、というのです。

引き続き、上の時計企業でみていきますと、

労働者一人当たりの実質賃金は30個でした。
そして、労働者が10人居たとして、そこから10人→11人になると、新たに50個生産量が増えるとしました。

このとき、30個分の給料を払えば、50個生産量が増えるのですから、企業はその11人目を雇った方が20個分得をします。なので雇います。

次の12人目はどうでしょう。

限界生産物は逓減するとの仮定から、例えば、先ほどよりも1個少ない49個生産量が増えるとします。ならばこのときも、その12人目を雇った方が19個分とはなりましたが、得をするので雇います。

さらに、13人目は48個・・・14人目は47個・・・

と続けていくと、“もう一人雇うと実質賃金と同じ30個生産量が増える”というところで差分がゼロとなり、雇い止めとなります。

なぜなら、そこからさらにもう一人雇ってしまえば、30個分の給料を払っても、29個しか生産量が増えないため、１個分損をしてしまうからです。

よって、例の時計企業の場合は31人で雇い止め、つまり雇用量は31人に決まるのです。図示すると

図２

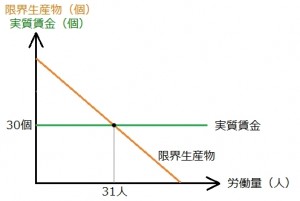
横軸に労働量、縦軸に実質賃金と限界生産物。
橙で表した限界生産物は、労働量が増えるほど少なくなるので右下がり。
緑で表した実質賃金は所与で一定（水平）。
その交点で雇用量（労働需要）が決まると。

 

このように、企業が利潤最大化行動をとる結果、実質賃金と労働の限界生産物が等しくなるように雇用量（労働需要）が決まる、ということになります。
（ただし、“生産物はすべて売れる”という仮定があります～セイの法則）

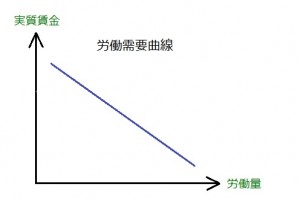
これを基に、縦軸に実質賃金、横軸に労働量を取り労働需要曲線を描くと

図３

このように右下がりのグラフとなります。

縦軸に独立変数をとるこのようなグラフは大変扱いづらいのですが、経済学では慣例なので我慢しましょう。

さておき、このグラフが示すのは、
“実質賃金が下がると労働需要は増えていく”
ということです。上の話を整理すると、当然そうなります。

また図２は、一企業の労働需要曲線でしたが、市場全体を考えるときには、ミクロの完全競争市場の需要・供給曲線の場合と手法は同じです。
すべての企業のものを横方向に足し合わせて・・・といったように。
要するに、市場全体も図2の形状で考えるということです。
（この辺は仮定の域なので、あまり深く考えない方がいいです）

 

ちなみに以上が、平成26年度第13問の設問2で問われた全容です。
その正答率はおそらく50％を割っているでしょうが、この第一公準、労働需要といった辺りは、いずれまた出題されるのではないでしょうか。

 

古典派の労働供給

労働供給、今度は“家計がどのくらいの労働量を供給しようとしているか”ということです。

家計が効用最大化行動をとる結果、『古典派の第二公準』を満たすように労働供給は決まるというのですが、その公準というのが以下。

『労働の一定量が雇用されている場合、
実質賃金の効用はその雇用量の限界不効用に等しい』

 

実質賃金の効用とは
“実質賃金から得られる満足度”です。

その雇用量の限界不効用とは、
“労働量が1単位増加したときに増える不効用”です。
不効用とは、効用（満足度）の反対。
不満度、不快度、苦痛といったようなことです。

そこで、第一公準では、労働量を“人数”で考えましたが、第二公準では、“労働時間”で考えた方が分かりやすいでしょう。

つまり、実質賃金の効用を“時給から得られる満足度”
その雇用量の限界不効用を“もう1時間多く働いたときの苦痛の増加分”といった感じで捉えます。

そして、その雇用量の限界不効用は、一般的には、労働時間が多くなるほど大きくなります。
例えば、3時間働いた後のもう1時間と、12時間働いた後のもう1時間、通常は後者の方がきついです。

 

さて、第二公準ですが、考え方は第一公準と良く似ています。

要するに、
「さらにもう1時間多く働くのは大変苦痛だ。でも、それよりも時給から得られる満足度の方が高ければ働いてもいい。そうでなければもちろん働かない。」
というようなことです。つまり

・実質賃金の効用＞限界不効用　のときは、もっと働く
・実質賃金の効用＜限界不効用　のときは、働かない

そうすると、
【時給から得られる満足度＝もう1時間多く働いたときの苦痛度】
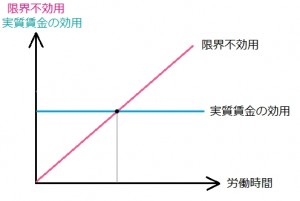
となるところで“働き止め”となる。図示すると

図４

横軸に労働時間、縦軸に実質賃金の効用と限界不効用。
ピンクで表した限界不効用は、労働時間が多くなるほど大きくなるので右上がり。
水色で表した実質賃金の効用は、実質賃金が所与ならば一定（水平）。
その交点で労働時間（労働供給）が決まると。

 

確かに考え方は良く似ていますが、第一公準と比べても、少々感覚的で歯切れが悪いといいますか・・・ですよね。分かりづらい。

その理由は、基数的な実質賃金と序数的な効用（不効用）を同列に扱おうとしているからでしょうね、たぶん。

ちなみに基数とは“量を計る数”で、序数とは“順序付けを表す数”。
これが混ざると間違いも起こりやすくなります。

例えば、こんな問題。

1階から3階まで行くのに8秒かかるエレベーターがあります。
そのエレベーターで1階から6階まで行くのに何秒かかるでしょうか？

 

答えは、20秒。

とっさに　16秒　と答えた方。
この問題の、階数が序数、時間が基数なんですね。
そこで少々混乱してしまうのです。
日付で、12月7日から12月22日までは何日間？
というのも同じようなことで、一瞬考えてしまいます。

 

話を戻しまして、労働の一定量が雇用されている場合、実質賃金の効用はその雇用量の限界不効用に等しくなるなるように労働供給は決まる、と。

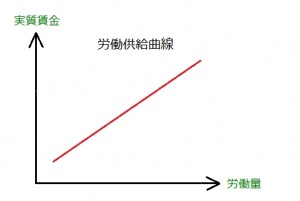
これを基に、縦軸に実質賃金、横軸に労働量を取り労働供給曲線を描くと

図５

このように右上がりのグラフとなります。

このグラフが示すのは、
“実質賃金が下がると労働供給は減っていく”
ということです。

また、市場全体のものは、労働需要曲線のときと同様です。

 

古典派の労働市場

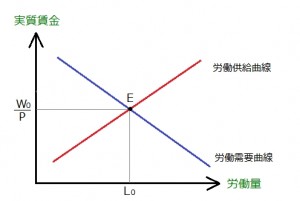
労働需要曲線と労働供給曲線を同時に描くと

図６

このようになります。

第一公準、第二公準が正しいとすると、労働市場において実質賃金は伸縮的であり、市場のメカニズムによって点Ｅで均衡する。
そして、常に完全雇用（＝働きたい人がすべて働いている状態）が実現している、ということになるのです。

なので、仮に失業者がいるとすれば、それは
①　企業と労働者のマッチングに時間を要するもの（摩擦的失業）
②　何らかの理由で労働者に働く意思がないためのもの（自発的失業）
であると。
（①は、労働者が自分に適合した職を見つけるのには時間がかかり、その職探しの間は失業状態もやむ得ない、といった感じです。例えば、転職の最中の働いていない期間など）

そして、もしこの均衡状態から労働量を増やしたいのであれば、
・組織を改善したりして摩擦的失業を減らす
・労働の苦痛をやわらげて自発的失業を減らす
などなどするしかないと。

さらに言うならば、世界恐慌期の多くの失業者についても、例えば、
「労働者側が、正当な名目賃金の引き下げを受け入れないからで、それは自発的失業だ」
などと解釈されるのです。

これが、古典派の雇用理論です。

 

ケインズの批判

以下は、簡潔に。

「実際には、現行の賃金水準で働きたいけど働けない人（非自発的失業）もいる。」

というのがケインズです。
よって、古典派の雇用理論はどこかに誤りがあるはずで、
それが第二公準だと言いました。（ちなみに第一公準は否定しません）

具体的には、
「第二公準では、労働者は実質賃金によって労働供給量を決めるとしているが、実際の雇用契約は名目賃金によって結ばれるのであって、そもそもそこが間違っている。例えば、物価が上昇すると実質賃金は下がるが、そこで労働者は労働供給量を減らすだろうか。あくまでも、労働者は名目賃金によって労働供給量を決めるはずだ。」
とこんな感じです。

第二公準、要するに、古典派の労働供給曲線が違うというのですが、ならばどのようなものかといえば

図７

このような感じで考えていたのではないかと。
（とあいまいに言うのは、当批判をしているケインズの著書にその考えを示すグラフは出てこないので、識者が文章を読み解くと・・・となってしまうためです）

先ほどの通り、縦軸には名目賃金。
現行の賃金水準 $W0$で働きたい労働者が $Lf$人いるとして、
それまでは水平で表される。
その後、つまり完全雇用を実現できた後は、
労働供給が一定となり垂直で表される。
（この垂直部分を右上がりとしているものも見ます。議論の中心はそれ以前になるでしょうからあまり気には、と）

 

そして、非自発的失業が発生しているということは

図８

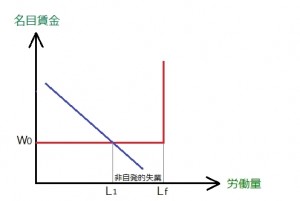
労働需要曲線が、このような状態にあるのではないかと。
グラフの $(Lf-L1)$ が非自発的失業を表しています。

だとすると

図９

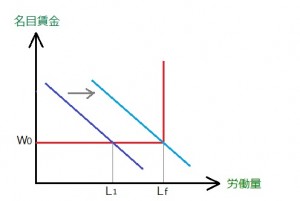
こうなれば、非自発的失業を無くし完全雇用を実現できる。

どうすればいいのか？

それは、“生産物への需要を増加させて生産量を増やせばいい”と。
つまり、非自発的失業の発生要因は、労働市場ではなく財市場にある。
そして、財市場においては生産物への需要量がその供給量を決定し、ひいては雇用量も決定するのだと。

これが『有効需要の原理』です。

 

ではその思想を基にして、どのように需要量が決定し、さらには、どうやってそれを増やしていけばいいのか、考えてみましょう。
というのが、中小企業診断士テキストでも丁寧に扱う、ケインズ型消費関数、45度線分析といった辺りです。
このように労働市場からみていくと、例えば、デフレギャップの説明もよく解るのではないでしょうか。

 

以上です。
中小企業診断士試験で出題される可能性が高いのは、第一公準です。
【利潤最大化行動：　実質賃金＝労働の限界生産物】
最低限ここはおさえておきましょう。

それでは、また。　　Ｘレイ