【経済学】 1.出題領域とグラフの性質
こんにちは、 Xレイ です。
5月に入りました。
これから一次試験まで、私は経済学を中心にお話をしようと考えています。
まず今回は 1.出題領域とグラフの性質 です。
・出題領域
中小企業診断協会のHPには、過去8年分の問題が掲載されてます。
経済学に関して出題領域をまとめてみました。(PDF)
(領域区分・論点等は個人的見解です。使用に関しましては自己責任でお願い致します。※H27.10.1 H28年度版に改訂)
改めて解いてみたところ、
最も易しい年=26年度
最も難しい年=25年度
との所感です。
それでは、今年27年度はどうなるか。
『昨年よりは難化する』との予測が適当でしょうか。
ならば、対策は?
『頻出領域・論点をしっかりおさえておく』
そのうえで、時間に余裕があるならば
①頻出領域からの出題を確実にしとめるため、さらに理解を深める
②他に出題されそうな領域を予測し、手広く構える
といった選択に迫られるのでしょうか。
いずれにしても、まずは『頻出領域・論点をしっかりおさえておく』ことは重要でしょう。
そこで、領域毎におさえるべきポイント等をまとめいこうと考えています。
1回では収まらないので、数回に分けて行うことになりそうです。
その前に今回は、経済学のグラフの整理。
『経済学では、性質の違うグラフが混在している。
よって、すべてを一つのアプローチで理解するのは難しい。』
このように考えております。
まずは、そこを確認しておくのはいかがでしょうか。
・グラフの性質
さて、中小企業診断士試験経済学で扱う主なグラフ等を、4つに分類してみます(名称・区分等は独自のもの)。
1.数学型関数グラフ
2.縦軸独立変数型グラフ
3.3次元→2次元化グラフ
4.その他ダイアグラム
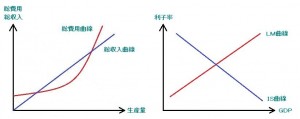
【1.数学型関数グラフ】
図1
『横軸の値が決まると縦軸の値も決まる』といったグラフ。
数学的には、横軸が独立変数、縦軸が従属変数となっています。
学生時分より慣れ親しんだ、スタンダードな型といえるかと。
数学が得意という方は、大歓迎の型でしょう。
まずは、グラフから直感的に情報を得やすい。
そして、直線や曲線を一般形に表せれば、水準の経済学的知識をもって、
数学の問題化しやすい。
一般形とは、例えばIS-LM分析においては
IS曲線 $i=-\frac{1-c}{b}Y+\frac{-cT+A+I+G}{b}$
LM曲線 $i=\frac{a}{b}Y+\frac{c}{b}-\frac{M}{bP}$
というように。
(数式表記にmathjax使用。環境により表示に不具合あり)
過去8年の出題では
(ミクロ) 費用関数・収入関数・生産関数・期待効用仮説
(マクロ) 45度線分析・IS-LM分析・マンデルフレミングモデル
といったところです。
【2.縦軸独立変数型グラフ】
図2
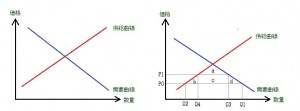
需要曲線・供給曲線やその延長線上にあるグラフ。
価格が数量を決めるという前提で扱うとき(完全競争市場)
縦軸が独立変数 横軸が従属変数 となっています。
つまり『縦軸の値が決まると横軸の値が決まる』といったグラフで、
1.数学型 とは縦・横逆です。
数学では慣例で、定義域と値域を入れ替えるところです。
要するに、縦軸と横軸を書き替えてしまいます。【逆関数の概念】
しかし、経済学ではこのまま考察します。
そのため、価格弾力性といったような概念をグラフからイメージしづらいのです。(私だけかもしれませんが)
そして、余剰という概念で見たときには縦・横一転します。
そうなると、1.数学型 と同様に横軸を独立変数として捉えられます。
例えば、『自由貿易の理論』のグラフ(図2右)の考察では、頻繁にその余剰を問われます。
また、不完全競争におけるプライスメイカー(独占企業等)も、横軸(生産量)を独立変数として捉えることができるでしょう。
過去8年の出題では、
需要曲線・供給曲線 自由貿易の理論 独占市場 独占的競争
負の外部性 費用逓減産業 (いずれもミクロ)
といったところです。
【3.3次元→2次元化グラフ】
図3
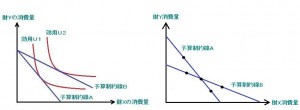
無差別曲線と予算制約線等のグラフ。
(厳密に言うとダイアグラムなのでしょうが以降もグラフと称します)
これは、上記1.2.とは別物です。
その成り立ちは以下。
まず『2財の数量が効用を決める』という効用関数は、3次元関数です。
それは『横軸・縦軸が共に決まると高さ軸が決まる』といったグラフ。
しかし、3次元のまま、様々な分析を行うのは大変です。
そこで、2次元化するのに無差別曲線という概念を使います。
その無差別曲線とは、同じ効用水準を2次元で表したもの。
すなわち、3次元効用関数のグラフをX-Y平面と平行な面で切り取って得られる曲線、それを上から見て2次元に投影させたもの、と捉えることができるでしょう。
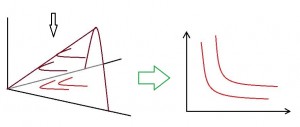
その無差別曲線と、通常それと接するような予算制約線をもって、先のグラフ(図3左)の完成です。
ちなみに、時折見かける図3右のグラフ(顕示選好理論)は、いくつかの効用を点で表したもの。3次元に変わりはありません。
重要なのは、3次元を2次元化して分析しているというところ。
つまり、この種のグラフは3つの変数を持っています。
例えば、X財の消費量:x Y財の消費量:y 効用:uといったように。
この予算制約線・効用・無差別曲線関連の問題は、毎年出題されています。
【4.その他ダイアグラム】
ダイアグラムとは『ある情報を2次元に可視化したもの』。
よって、3.のグラフも厳密にはダイアグラムというわけです。
過去に問われたものは
・エッジワースのボックスダイアグラム
~H25年の第20問 H26年の第17問 の2回
・寡占モデル(没問) ~H22年の第18問
・労働移動の効果を示したという ~H23年の第10問
いずれも、2つのグラフを合体させた型といえるかと。
出題頻度から考えても、あまり深入りなさらない方がよいのでは
と考えています。
このように経済学では、性質の違うグラフが混在しています。
そのため、同一のアプローチでは、理解し難いかもしれません。
次回から、各々グラフにおいて実際に問われた論点を基に、最低限おさえておきたいポイントをまとめまていきます。
それでは、また。 Xレイ