【経済】ミクロ経済～消費者行動の基本整理

こんにちは。こぐまです。

まず、念のために。

1次試験の申込受付は6月4日（月）までです。
絶対にお忘れなく！
特に郵送で試験案内を請求される方、請求は5月28日（月）必着です。遠隔地の方はご注意ください。
詳しくはこちらをお読みください。

 

さて今週は経済ウィーク。
経済は、財務・会計と似ているところがあって、しばらく離れてしまうと途端に解けなくなってしまう科目です。
理解したつもりなのに・・・という現象が起こりやすいですね。

しかしここまで来ると、この完成答練期の1週間以外に集中して取り組める時期はもうありません。

目安としては、この時期に平成19年度と23年度の本試験問題を60点以上、完成答練で70点以上を取れる実力をつけておけば、完成答練終了～模試までの1週間、模試～本試験の1ヶ月間の学習方法を工夫すること（←これはいずれまた）で、模試や本試験をクリアできるだけの力を保持することができると思います。

過去の多くの記事にもあるように、各理論の結果を覚えつつも、そこに至るプロセスを理屈で理解することなしには得点獲得力の確実性を高めることはできません。

上記に示した2つの過去問は、そのことを示す問題が揃っていますので、比較的難易度の低かった、平成20年度と21年度の問題を消化した上で取り組んでみるとよいと思います。

 

◆消費者行動の基本論点◆

ミクロ経済の入り口である「消費者行動」で登場する理論や論点は、結構、知ってるつもり、わかっているつもりでいても、ちょっと応用されると対応が難しい問題が出ることがあります。
改めて、それぞれの意味を理屈で理解しておきましょう。

大前提として「個人は予算の制約のもとで効用を最大化する存在」であると仮定し、経済学の性質上、2つの財・サービスを消費する消費者（家計）をモデル化することで原理を単純化しています。

「効用」を一般的な言葉にすると、「満足度」といったところでしょうか。

 

（出典：　Wikipedia）

◆予算線◆

上記のとおり、消費する財・サービスは2種類のみ、財の価格は所与であること（プライステーカー）を仮定しています。

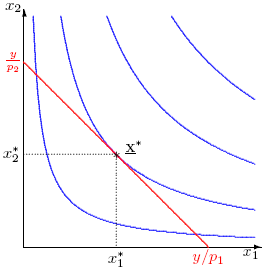
財をX1とX2（りんごとみかんでもいいです）、家計所得（＝予算）は一定とすると、横軸X1の消費量、縦軸X2の消費量のグラフは右下がりの直線となります。
これが予算線（上図の赤線グラフ）で、傾きは「-ΔX1/ΔX2」（2財の価格比）です。

この理屈は簡単ですよね。
当然のことですが、この予算線より上は購入不可能な領域です。

 

◆無差別曲線◆

基本中の基本ですが、これが何を表しているものなのか、ご自分で説明できるでしょうか？
いかにも経済学的用語で日本語としてどうかと思いますが、学問でそう決まっているのでしょうがない。
ミクロ経済の中で非常に重要な基本論点です。

無差別曲線とは、家計が同じ効用（満足度）を得られるX1財とX2財の消費量の組み合わせ（消費点）をプロットしたものですね。
同じことを繰り返しますが、同じ無差別曲線上にあるどの点においても家計にとって同じ効用水準を得られる消費点の集合、要は「どこでもいい」ということです。

効用水準（満足度）は何で決まるのか？
経済学では、財の消費量が多いほど、また2財の消費バランスがとれているほど、効用が高いと仮定しています。

同一線上にある限り、効用水準は同じなので、効用「無差別」ということなのでしょうかね。

無差別曲線の性質は次の4つです。重要です。

①右下がりの曲線
②原点に対して凸型
③原点から遠い無差別曲線ほど効用水準が高い
④個々の無差別曲線は交わらない

これらの性質・特徴については、感覚的な理解でも十分だと思いますので、ややこしい計算式で考えるより、なぜそのような形を描くのかを理解しておきたいです。

それが本番での現場対応力をアップさせる力になります。

①X2財の消費を減らしたら、効用水準を維持するためにX1財の消費を増やす必要があるので、自然に右下がりとなります。
消費者行動としてこれは当然かと。

②上記①から、X1財（たとえばりんご）の消費が増えるほど、もう一方のX2財（みかん）の消費が減りますね。
感覚的に考えても、同じものに偏って消費するのは飽きがきます。

ですから、りんごの消費が増えて行くにつれ、代替財であるみかんの消費の減り方が緩やかになり、効用水準を同じに保とうとするわけです。

要は、りんごばかり食べるより、少しはみかんも食べたいよね、ということを表しているのですね。

その結果、無差別曲線は右下がりの性質に加え、形状として原点に向かって凸の形をとることとなります。

これは「限界代替率逓減の法則」という、これまたわかりにくい日本語の法則が関わっています（後述）。

③これは前提としている、「財の消費量が多いほど効用が高い」ということそのままで、無差別曲線は無数に存在します。

そして、原点から遠い無差別曲線ほど2財の消費量は多くなります。
つまり、無差別曲線がグラフの右上にあるほど効用が高いということです。

④仮に効用水準が10と20の2つの無差別曲線を考えてみます（ここでいう10、20は数学的な数値ではないです）。

もしこれらが交わったとしたら、交点においては同じ数のりんごとみかんの消費の組み合わせであるにもかかわらず、異なる効用を与えるということになり、矛盾を起こしてしまいます。

 

◆限界代替率◆

どこかでも出てきた「限界」。直観的にわかりにくい言葉ですね。
英語ではmarginalで、りんごを1個（単位）減らした時に、代替財であるみかんを何個（単位）増やせば同じ効用が維持できるのか、を表す比率です。

グラフでいえば、無差別曲線のある一点における接線の傾きです（数学的には無差別曲線を微分したもの）。

上記②のとおり、無差別曲線は限界代替率が逓減することにより、原点に対して凸型の形状を示すこととなります。

 

◆最適消費点◆

消費者の効用（満足度）が最大になる2財の組み合わせの一点を「最適消費点」といいます。

・右上にある無差別曲線ほど効用が高い。
・消費者は、所得（予算）の範囲でしか消費できない。

という条件を考えれば、最適消費点はどこか、自ずと答えは出てきます。

上図の、予算線と無差別曲線の接点であるＸ*です。

 

◆代替効果と所得効果◆

これは多くを語る必要もない、定番中の定番論点。
この記事も参考にしてください。

ただ、この応用論点として、「労働供給曲線（バックワード・ベンディング）」と「異時点間の消費」があります。
過去問は、前者が平成18年第12問と20年第18問、後者が平成19年第16問と22年第2問（設問2）です。

いずれも難問の部類に入り、後回しにすべき問題だろうと考えます。

そもそもこのモデルは、2つの財の消費を前提としたものです。

上記の2論点も、財ではないにしろ、所得と労働時間、消費と余暇（時間）、現在の消費と将来の消費など、2つの要素を財に見立てて関連付けたものであり、診断士試験の範囲における消費者行動の最深論点ともいえます。

逆に言えば、上記に述べた基本論点を丸ごとすべて積み上げたような応用論点であり、一度は解いておいてはいかがでしょうか？

最深の論点をときほぐし分解することで、逆に基本論点が身に染みるように理解できるのではないかと思います。

無責任なことを言ってしまいますが、過去の出題傾向から見ても、今年はどちらかの論点が出題されそうな気がしています。
でも、キリがないのでこの応用論点を完璧に解けるようにしておく必要はないです（もっと基本的な論点を優先すること）。

ただ、上記に挙げた過去問を、消費者行動の基本論点を身に付ける 「材料」としてみてはどうでしょうか、ということですので、誤解なきよう。

 

◆最後に◆

経済もやはりスピ問が良問揃いで、これを完璧にやっておけば本試験も十分な点数が取れるのではないかと思います。

私は、受験校の経済学の講義と教材が非常に良かったため、（また時間もなく）この科目についてはスピ問はやりませんでしたが、立ち読みした感じでは、やはり優れモノですね。

by こぐま