6つの係数を完璧に覚える方法 ~正味現在価値または資産運用~ by にに

☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆
一発合格道場ブログを
あなたのPC・スマホの
「お気に入り」「ブックマーク」に
ご登録ください!
☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆
はじめに

こんにちは!にに です。
昨日、1月22日は、2次口述試験の実施日でしたね。
受験されたかた、たいへんお疲れさまでした。
無事会場に行って試験官と対話できたのであれば、ほぼ間違いなく合格していることと思います。
口述試験より前に実務補習の募集が始まるくらいだからね

そんなわけで、これからは、忙しくも楽しい診断士(登録予定者)ライフが始まりますよ。
自分で勝ち取った権利です。思う存分活用してください!
さて一発合格道場では、そんな診断士ライフの始まり、あるいは今年度の受験の終了の区切りとして、「試験お疲れ様会」を開催します!
合格したかたはもちろん、残念ながら今年度は不合格だったかたも、一発合格道場ブログを読んでくださっているかたならどなたでもご参加いただけます!
また、受験体験記も募集中です!来年度以降の受験生のためにも、あなただけの経験を文字にして残してみませんか?
受験体験記の募集は、道場14代目の募集も兼ねているので、道場活動に興味のあるかたは必ずご応募ください!
そして、今年度は残念な結果だったかた、あるいは来年度初受験を考えているかた。
来年度の試験の日程はまだ発表されていませんが、例年どおりならあと7ヶ月程度で1次試験、その3か月後に2次筆記試験です。
長そうで短いその期間のペースメーカーとして、一発合格道場のブログやセミナーを活用していっていただければと思います。
今日は、1次試験・2次筆記試験でよく出てくる、あの数字についてのお話です。

ようやく本編のスタートです
6つの係数
2次筆記試験を受験されたかた、あるいは勉強をされているかたには、以下の表はおなじみかと思います。
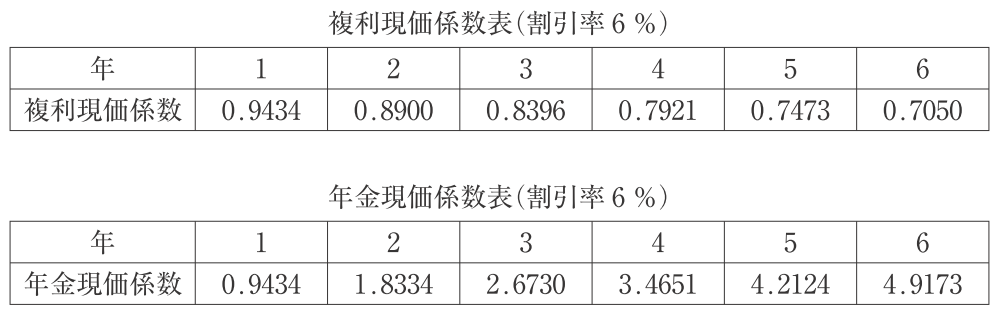
事例ⅣのNPV問題で、投資案から得られるキャッシュフローの現在価値を求めるとき、かなりの確率でこんな感じの表がくっついてきます。
この表は平成28年度の事例Ⅳからの抜粋ですが、「複利現価係数」と「年金現価係数」という2種類の数字が記載されていますね。
では、こちらはどうでしょうか。
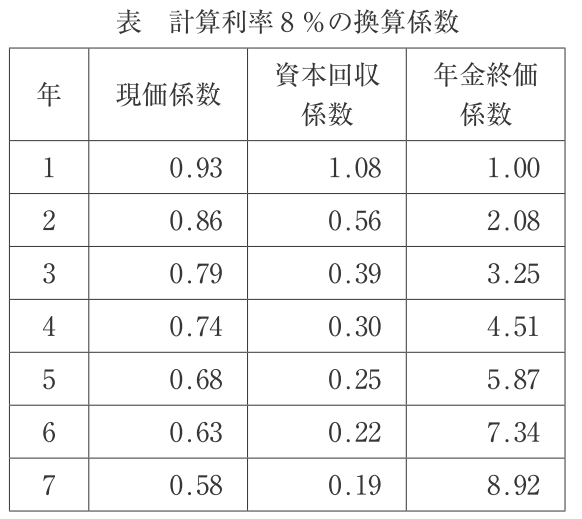
令和元年度の1次試験の運営管理の第19問です。
「現価係数」のほかに、「資本回収係数」「年金終価係数」の数字が記載されています。
「複利現価係数」と「現価係数」は同じものを指しているので、都合4つの「係数」が出てきました。いずれも語尾に「係数」とついていることから想像できるとおり、おなじ仲間に属するものたちです。
そして、その仲間たちは4つだけかというと、実はもう2つあります。
それは「終価係数」、そして「減債基金係数」というもので、これらを合わせて「6つの係数」と呼ばれています。
ファイナンシャル・プランナー(FP)の試験では、資産運用に関する論点として6つすべて頻出なので、ご存じのかたもいるかと思います。
診断士の試験では、過去16年間の問題を調べてみたところ、1次・2次合わせて上記の4種類しか出題がありませんでした。(にに調べ・抜けがあるかもしれません)
中小企業診断士試験においては2次筆記試験で必須の現価係数・年金現価係数以外はそれほど出現率は高くありませんが、令和元年の1次試験(しかも運営管理!)のように突然出題される可能性もあります。
なので、この機会にまとめて全部覚えてしまいましょう!というのが、今日の記事の主旨です。
それぞれの係数の意味と関係、それとお土産、この3部構成でお届けします。
6つの係数の意味
全体像
これらの係数は、FPの試験では資産運用、診断士試験ではNPV(正味現在価値)というシチュエーションで出てくることが多いです。
どちらのシチュエーションも、ある利率のもと、ある期間において、元本と期間経過後のそれぞれの金額の関係を計算する、という点で共通しています。
そして、その期間においては、手元のお金は常に複利で運用されています。
※NPVの文脈においては、将来→現在という時間軸で見るので「利率」ではなく「割引率」という表現になりますが、表すところとしては同じです。

これは6つの係数すべてに共通の前提のため、いずれの係数もパラメーターとして「利率(割引率)」、そして「期間」が設定され、その組み合わせで具体的な数値が決まります。
たとえば、「利率8%、期間5年」のときの現価係数は「0.68」といったかたちで表されます。
この記事では、利率を r (%)、期間を n (年)という文字で表すことにします。

ここから先は、個別の係数のお話です
(複利)現価係数
まずはこれ、2次筆記試験事例Ⅳでも出てくる「(複利)現価係数」です。「(複利)」はついていてもついていなくても同じ意味です。この記事では、「現価係数」と表記します。
この係数は、ある期間経過後に目標の金額に到達するために、元本がいくら必要かを表すものです。
図で表すと、以下のようになります。縦軸は省略していますが金額を表していて、横軸が時間経過です。左から右に向かって、現在→将来と経過することを表しています。
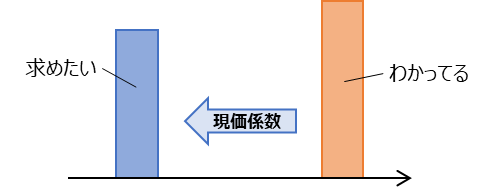
横軸の時間の流れの間は、常に複利で運用されています。
将来の目標とする金額から、現在必要な金額を求めるための係数ということですね。
現価係数を算出する式は、
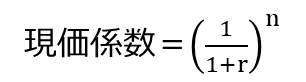
です。
r は利率(または割引率)でだいたい数%くらいなので、仮に5%とすると、「 1 + r 」は1.05になります。n は期間(多くの場合、年数)です。
つまり、現価係数は「『1÷1.05とかそのくらい』のナントカ乗」なので、ざっくりと「1よりちょっと小さい」とイメージしておくと良いです。
終価係数
終価係数は、過去16年の本試験では出題がありません。なので、診断士試験のテキストには載っていないかもしれません。

ちなみに私が使っていた某通信講座のテキストには、現価係数と年金現価係数しか載っていませんでした
どういったものかというと、現価係数と逆で、元本がわかっている状態で、ある期間経過後にいくらになっているかを表しています。
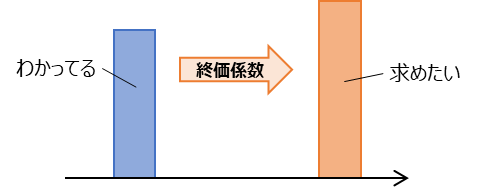
終価係数を算出する式は、
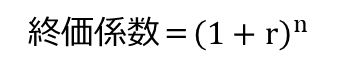
です。
現価係数のときと同じように考えると、「1.05とかそのくらいのナントカ乗」なので、「1よりちょっと大きい」とイメージできます。
年金現価係数
年金現価係数は、現価係数と並び、事例Ⅳで超頻出のものですね。
事例Ⅳでは将来にわたって一定額得られるキャッシュフローを現在価値に割り引くために使いますが、名前から読み取れる本来的な意味は、将来一定期間にわたって同一の額を取り崩していくために元本としてどれくらい必要か、ということを表しています。
「同一の額」ということは、まさに年金ですよね。その年金の元手となる金額を知るためのものです。
図では、このように表されます。

オレンジの背が低い縦棒が、金額がわかっている年金(NPV的には、毎年得られるキャッシュフロー)の部分です。1年分の金額が計算の元となります。
年金現価係数の計算式は、
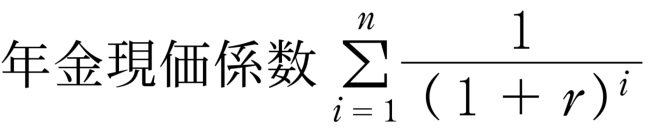
です。(覚える必要はないと思うので薄くしておきました)
めちゃくちゃ複雑な式ですが、実はこれ、平成19年度の事例Ⅳの問題用紙から持ってきたものです。
昔はこんな感じで出題されていたんだね

この式自体はまったく覚える必要はありませんが、こんな形で表されることだけは知っておくと、いざというときに慌てなくても済むかもしれません。
ちなみに値としては、「だいたい、 n よりちょっと小さい」的なイメージです。
年金終価係数
年金終価係数は、年金現価係数と逆に、毎年同一の額を運用しながら積み立てていったときに、最終的にいくらになるかを表す係数です。
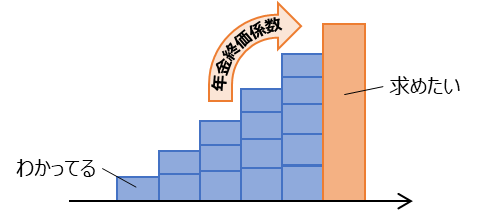
最近は投資がブームなので、この係数は実生活での出番が多いのかもしれません。毎年(など一定期間)、定額を積み立てていったときに将来いくらになるか、生涯設計をする際に活用できますね。
これも、積み立てる1回当たりの金額を計算の元にします。
式は、以下のとおりです。

これも式を覚える必要はありません。
値は、「だいたい、n よりちょっと大きい」です。
資本回収係数
資本回収係数は、元本がわかっていて、それを一定期間に分割して受け取るときにどれくらいもらえるかを表しています。
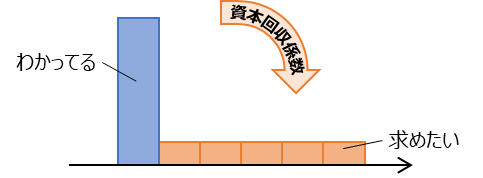
あるいは診断士試験的には、名前があらわすとおり、最初にいくらかの投資をして、それを回収するために毎年どれくらいのリターンが必要か、という方が理解しやすいかもしれません。
ここ15年で唯一出題された令和元年度の1次試験運営管理の第19問でも、まさにこのかたちで出題され、資本回収係数を使う選択肢が正解となっていました。
式は、
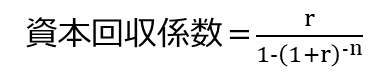
です。複雑すぎて、書くのもいやになってきました。決して覚えないでください。
値は、「1 / n よりちょっと大きい」です。
減債基金係数
6つの係数の大トリは、減債基金係数です。
名前からして複雑ですね。どういったものかというと、ある目標金額を達成するために必要な、毎年の積立金額を知るためのものです。
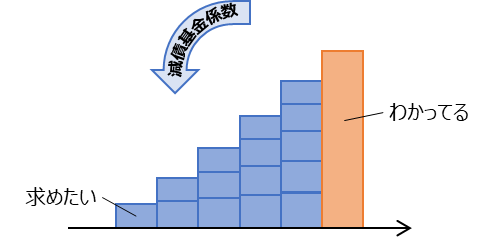
もうみなさん見たくないと思いますが、式は
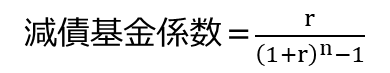
です。
値は、「1 / n よりちょっと小さい」となります。
余談 ~減債基金係数の名前について~
私はFP2級の資格を取得して2年ほど経ちますが、恥ずかしながら、今の今まで「減債基金係数」がなぜこんな変な名前(失礼)なのか、まったく知りませんでした。
さらに輪をかけて恥ずかしいことに、知らないのに知ろうともしていませんでした。

反省しています
というわけで、今回の記事を書くにあたって調べてみました。
すると驚くべきことに、「減債基金」という言葉がもともとあったんです!
・・・いやそんなの常識じゃん、とおっしゃる向きもあるかと思いますが、私は全く知りませんでした。
減債基金とは、府債の償還財源を確保し、財政の健全な運営に資するための資金を積み立てることを目的に設置された基金です。
大阪府「減債基金について」より引用
というわけで、借入金を満期時に償還する際に多額の財源が必要になるため、償還財源を事前に積み立てておくための基金、ということですね。
まさに、減債基金係数の図が表しているとおりのもので、これを計算するためのものなので「減債基金係数」というのだなぁと、とても納得できました。
6つの係数の関係
さて、6つの係数それぞれの意味は上記のとおりですが、ここからは、複数の係数の間の関係性を見ていきたいと思います。
現価係数と年金現価係数
まずは、診断士の試験、特に2次筆記試験でほぼ必出の現価係数・年金現価係数の関係です。
この2つは、「現価係数を1年目からすべて足し合わせると年金現価係数になる」という関係になっています。

冒頭の表を再掲しましたが、1年目は「年金現価係数 = 現価係数 = 0.9434」です。
2年目で見ると、「年金現価係数 = 1年目と2年目の現価係数の合計 = 0.9434 + 0.8900 = 1.8334」となります。
3年目も同様に、「年金現価係数 = 1年目から3年目の現価係数の合計 =0.9434 + 0.8900 + 0.8396 = 2.6730」です。以下すべて同様なので、お時間あるかたは確かめてみてください。
この性質と、現価係数のところで紹介した式を使うと、 年金現価係数は自分で算出することができます。
試しに、上記の例の場合の、7年目の年金現価係数を求めてみましょう。
まずは7年目の現価係数を求めます。
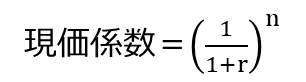
で、7年目なので n = 7 です。「7乗」は、元の数を7回掛け合わせるという意味なので、「元の数を6回掛け合わせた数に、さらに1回元の数を掛ける」とみることができます。
「元の数を6回掛け合わせた数」は6年目の現価係数そのもの、「元の数」は1年目の現価係数なので、上記の表の中にある数字で表すことができますね。
つまり、
7年目の現価係数 = 6年目の現価係数 × 1年目の現価係数 = 0.7050 × 0.9434 = 0.6651
となります。
そして年金現価係数は上記のとおり「現価係数の合計」なので、6年目の年金現価係数(=1年目から6年目の現価係数の合計)に7年目の現価係数を足し合わせて、
7年目の年金現価係数 = 6年目の年金現価係数 + 7年目の現価係数 = 4.9173 +0.6651 = 5.5824
というように算出されます。
この手の計算、実際に事例Ⅳで出題されたことがあります。平成22年度の第3問で、4年目の年金現価係数のみが設問で与えられていて、5年後までのNPVを求めよという出題がされました。
正確に言うと4年目の年金現価係数を使って「2年目~5年目のキャッシュフローの正味現在価値を求める」という形だったので、上記の計算とは少し違いますが、このあたりの計算に対応するためには、係数の意味をしっかりと理解しておく必要があります。
ちなみにこのときは、「金利 r = 0.06」のみが設問で与えられていて、
現価係数の式も覚えていなければいけませんでした

グルーピングする:①状況別
さてここからは、6つの係数全体の関係性を見ていきたいと思います。
上で6つそれぞれの意味や値についていろいろ書いてきましたが、正直それをそのまま覚えるのはコスパが悪いです。そこで、少しでも覚えやすくするために、いろいろ工夫をしてみます。
まずは、状況による分類です。
6つの係数は6つありますが、登場するシチュエーションは3つだけです。
その3つとは、
- 運用する
- 運用しながら使う
- 運用しながら積み立てる
です。
お気づきのかたもいると思いますが、6つの係数の説明のところに出てきた6つの図、実は3種類しかありませんでした。
3種類の図に対して、矢印の向きが逆になっている係数がそれぞれ2つずつあり、それで計6つの係数、というわけです。
突然ですが、ここでクイズです。上の図を見ずにお答えください。
問題:6つの係数を3種類に分類するときの組み合わせを答えてください。
選択肢は、
| 現価係数 | 終価係数 | 年金現価係数 |
| 年金終価係数 | 資本回収係数 | 減債基金係数 |
の6つです。
・
・・
・・・
答えはまとまりましたか?
では、正解を発表する・・・前に、ありがちな勘違い例から。
- 現価係数 & 終価係数
- 年金現価係数 & 年金終価係数
- 資本回収係数 & 減債基金係数
という組み合わせ、係数の名前的にはとてもしっくりきます。が、残念ながらこれは正しくありません。
「年金現価係数」と「年金終価係数」なんて、どこからどう見てもペアになるべき名前なのに、実は赤の他人なんです。
いや、いとこくらいの関係性はあると思う

ここが6つの係数の理解を難しくしているややこしいところだと、私は思っています。
でお待ちかね、正しい組み合わせは、
- 現価係数 & 終価係数
- 年金現価係数 & 資本回収係数
- 減債基金係数 & 年金終価係数
です。うしろ2つの組み合わせが変わりましたね。
覚えるのは、以下の2つだけで大丈夫です。
- 文字数が少ない2つ(現価係数と終価係数)がペア
- 残り4つのうち、「年金」がつくもの同士はペアにならない
とだけ覚えておけば(そして6つの係数の名前をちゃんと覚えておけば)、この組み合わせは一意に定まります。
それぞれの組み合わせを、あらためて示します。
現価係数 & 終価係数
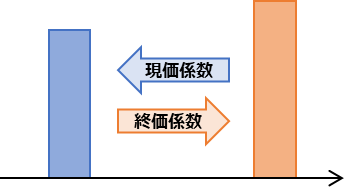
現価係数:ある期間経過後に目標の金額を達成するために、元本がいくら必要か
終価係数:元本がわかっている状態で、ある期間経過後にいくらになっているか
年金現価係数 & 資本回収係数
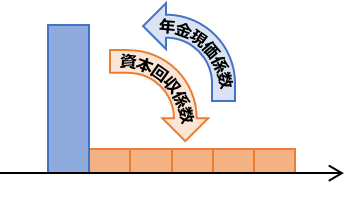
年金現価係数:将来一定期間にわたって同一の額を取り崩していくために元本としてどれくらい必要か
資本回収係数:元本がわかっていて、それを一定期間に分割して受け取るときにどれくらいもらえるか
減債基金係数 & 年金終価係数
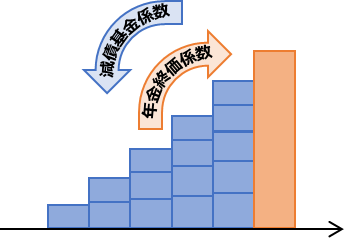
減債基金係数:ある目標金額を達成するために必要な、毎年の積立金額はいくらか
年金終価係数:毎年同一の額を運用しながら積み立てていったときに、最終的にいくらになるか
この3つの分類それぞれの中の2つの係数は、いずれも同じことを逆から見ているだけです。
現価係数と終価係数を例にとると、
現在の金額 = 現価係数 × 将来の金額
将来の金額 = 終価係数 × 現在の金額
となります。
なので数値としては、お互いに逆数の関係になっています。
グルーピング②:計算の目的別
もう一つのグルーピングとして、「計算の目的別」で分けてみます。
計算の目的とは、「何を求めるか」です。
状況別に分けたとき、それぞれの状況で矢印の向きが逆の2つがセットになっている、と言いました。
つまり矢印の向きによって、6つの係数を3つずつの2つのグループに分けることができる、というわけです。
そのやり方によって分けてみると、以下のようになります。
- 現価係数 & 年金現価係数 & 減債基金係数
- 終価係数 & 資本回収係数 & 年金終価係数
1つ目が、右から左、将来の金額から現在の金額を求めるもの、2つ目がその逆です。
こうやって3つ並べるだけだとわかりにくいですが、このグルーピングにはわかりやすい覚え方があります。
1つ目のグループにはいずれも「ゲン」が含まれていて、2つ目には「シュウ」が含まれているんです。
- 現価係数 & 年金現価係数 & 減債基金係数
- 終価係数 & 資本回収係数 & 年金終価係数
さらに、1つ目のグループの3つはいずれも「現在の金額」を求めるためのもの、2つ目は「将来の金額」を求めるためのものです。
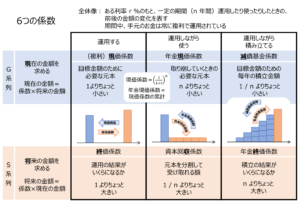
つまり、1つ目のグループは「現・現・減・現」なので「G系列」、2つ目のグループは「終・収・収・将」なので「S系列」とでも名付けましょう。
これらをまとめて、
現価係数・年金現価係数・減債基金係数は現在の金額を求めるためのもの = G系列
終価係数・資本回収係数・年金終価係数は将来の金額を求めるためのもの = S系列
というかたちで覚えてみてください。
まとめ(お土産あり)
6つの係数について、単体で解説したり、関係性を見てきたりしました。
単体で見るよりはそれぞれの関係性から覚える方がやりやすいですが、正直なところ、それでもまだ覚えづらいです。
というわけで、今日の記事をA4 1枚にまとめたお土産を用意しました!
6つの係数を、2種類のグルーピングに沿って3×2のマトリックスに配置してあります。
これ1枚だけあれば、6つの係数についてはカンペキといえる内容になっているので、ぜひご活用ください。
明日はまん です。お楽しみに!
です。お楽しみに!
☆☆☆☆☆
いいね!と思っていただけたらぜひ投票(クリック)をお願いします!
ブログを読んでいるみなさんが合格しますように。
にほんブログ村
にほんブログ村のランキングに参加しています。
(クリックしても個人が特定されることはありません)
告知① 試験お疲れ様会
今週末の土曜日、1月28日に、オンラインにて「試験お疲れ様会」を開催します!
「お疲れ様会」と銘打ってはいますが、
・今年度の中小企業診断士の試験を受験したかた
・来年度の受験を考えていて、情報収集したいかた
・その他、道場ブログを読んでくださっているかた
どなたでもご参加いただけます!
また、私たち道場13代目も、活動期間はあとわずかとなりました。
ブログを読んでコメントをくださったり、セミナーや懇親会で直接声を聞かせてくださったりしたみなさまへ、私たちからの感謝の気持ちを伝える場でもあります。
ぜひご参加ください!
試験お疲れ様会 開催決定!!

今回2次筆記試験の結果が出た方以外にも、道場ブログ読者なら誰でも参加できます。
これから診断士試験を受けようかと考えている方、現役の中小企業診断士などなど、みんな集まって試験について盛り上がろうぜ、といった感じです。積もる話はためこまず、ぱーっと吐き出しちゃいましょう。
ぜひご参加ください。
告知② 受験体験記募集
一発合格道場の強みのひとつは、「積み重ねられた数多くの体験記」です。
道場を形作るのは、皆さまの体験記。あなたの貴重な経験が多くの人たちのために役立ちます。
診断士1年目に本気になれる活動のひとつが、受験生支援です。
ぜひ、先代・我々とともに名を連ねてみてはみませんか??
合格・未合格体験記募集のお知らせ

申し込みはこちらからです。
あなただけのドラマ、あなただけの苦労、あなただけの受験のコツ、など、記念すべき受験体験を、歴史ある道場ブログの記事にしませんか?
未来の受験生のために、あなたの貴重な受験体験を教えてください!※合格・未合格は問いません
また、道場14代目を担ってくれるメンバーを合わせて募集します!
14代目を希望される方は2023年1月28日(土)までに申込みご提出ください。
14代目を希望されない場合は2023年2月4日(土)まで受付しています。