【渾身】経済(乗数理論と45度線分析)
☆もくじ☆
1.乗数理論と45度線分析の出題パターン
2.数式問題を簡単に解くテクニック
3.グラフ問題を簡単に解くテクニック
文字数:約1600字(本文だけなら約2分で読めます)
————————————————————–
こんにちは!頑張るあなたの応援団☆かわともです!
今日は珍しく雑談から。
私は4月から新たに財務部門に配属となったため、日々知識を増やそうとしています。上司の本を借りて読んでみたり、診断士試験の参考のために買った簿記1級の参考書を読んでみたり。
そんなとき「簿記1級を受けてみようか」と、ふと頭をよぎりました。スキマ時間にゆるっと勉強して軽い気持ちで受けてみようか、受からなくても身についた知識は仕事に直結するし、いいかも……。
……いやいやいや、待て待て!!
そこまで考えて我に返りました。試験合格を目指すならば、強い気持ちで「絶対合格!」と目標を定め、計画を立てて突き進むべきだと。春セミナーでもたっつーが「中途半端はダメ!」と口酸っぱく言っていたし、合格体験記でもみんな強い決意でストイックに勉強していたではないか……・
1次試験まで3ヶ月を切りました。仮に「運よく受かればラッキー」というノリの方がいらっしゃるならば、たった3ヶ月覚悟を決めてやりきることをおすすめします!絶対今年合格しましょう!!
なお、簿記1級を受けるかどうか腹が決まっていない私でした。。
* * * * *
本題です。
今日から約4週間にわたり、「渾身!論点シリーズ」として、1次試験の重要論点からメンバーが得意分野を選んで解説していきます♪
※毎年恒例のシリーズ企画ですので、よろしければ過去記事もご参考にしてみてくださいね。
第1弾は私、かわともが「乗数理論と45度線分析(経済)」についてお届けします!
なお、10代目で経済と言えばksknですが、私の記事はksknのような正統派の解説ではなく完全に解法テクニックの内容となっておりますので、あらかじめご了承ください。(理論の説明はすっとばしています)
1.乗数理論と45度線分析の出題パターン
乗数理論とは、「投資・政府支出・租税の変化が国民所得に与える影響について説明する理論」です。「均衡国民所得の決定」など関連論点も含め、代表的な出題パターンは2つに分かれます。
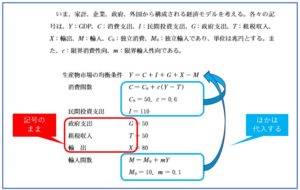
①数式の問題
Y=C+I+G+X-M みたいな式が出てくる計算問題
②グラフの問題
それでは早速、それぞれのパターンの問題の解法を見ていきましょう。
2.数式の問題を簡単に解くテクニック
【平成23年 第6問】を取り上げます。
(以下、図はクリックすると拡大します)

引用元:中小企業診断協会ホームページ(https://www.j-smeca.jp/)
それでは実際に解いてみましょう。
ステップ1:選択肢の中にある「変化するもの」に印をつけます。
ステップ2:印をつけたものはそのままにしておき、残りを全て数式に代入します。
ステップ3:代入後、数式を整理します。
整理を終えた後の数式を見てみましょう。さっき「そのままにしておいたもの」にくっついている数字が「乗数」です。
ステップ4:選択肢を1つずつ点検していきます。
ここでのポイントは、例えばイの「減税による影響を調べる」であれば、租税Tのみの変化の影響度を調べればよく、その他の余計な要素は除いて考えてもよいということです。全て代入するとごちゃごちゃしますので、シンプルに考えられますね。
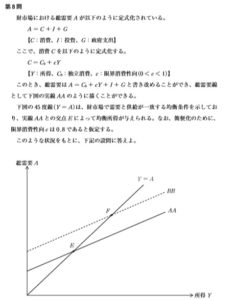
3.グラフの問題を簡単に解くテクニック
グラフの問題は、中学生で学んだ数学の知識を使えば感覚的にすんなり解けることがあります。
ここでは【平成28年第8問 設問2】をとりあげます。

引用元:中小企業診断協会ホームページ(https://www.j-smeca.jp/)
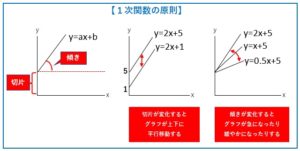
ここで、1次関数の前提となる基礎知識について軽くおさらいしてみます。
〇y=aX+b という式について、aが傾き、bが切片
〇切片が変化すると、グラフは上下に平行移動する
〇傾きが変化すると、グラフは急になったり緩やかになったりする
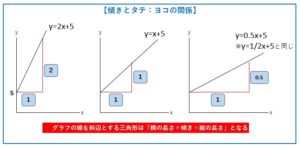
〇グラフの線を斜辺とする直角三角形は「ヨコの長さ×傾き=タテの長さ」となる
それでは実際に解いてみましょう。
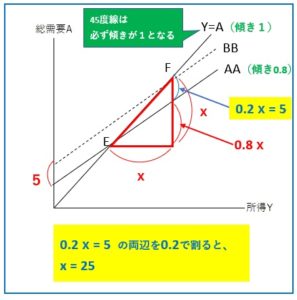
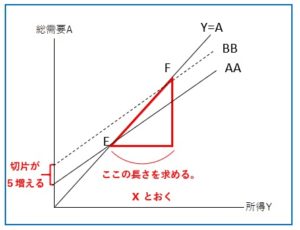
ステップ1:どこを求めればよいかを探し、xとおきます。
この場合はEからFに移動したときの所得の変化量となります。
ステップ2:I+Gの増加分を書き込みます。
総需要線の式は A=Co+cY+I+G であり、この式の傾きはc、切片はCo+I+Gですね。
「I+Gが5増加する」ということは、「切片が5増える」ですね。
ステップ3:「傾き×ヨコ=タテ」の原則を踏まえて、グラフを斜辺とする直角三角形の辺の長さを求めます。
・「45度線は必ず傾きが1」となりますので、三角形のタテはヨコと同じ長さで、X
・AAで区切られるタテの長さは、AAの傾き0.8×X=0.8X
・AAとBBの間のタテの長さは、増えた切片の分と等しいので、5
さらに、X-0.8X=0.2X となる
・0.2X=5 の両辺を0.2で割ると、X=25 となる
経済で解法がわからないグラフ問題が出てきた場合、今回の解説のようにちょっと視点を変えて図形的に考えてみると案外解けることがあります。よろしければお試しくださいね。
以上、かわともでした!
今日も明日も、皆さまにとって良い日になりますように。