【独学者向け】経済学解説②「消費者行動の分析」
✿:❀道場 春セミナー受付中✿:❀
東京セミナー 申し込みはこちら
4月6日(土) @港区勤労福祉会館
受付開始:13:30 セミナー開始:14:00 懇親会:17:00
東京セミナー(平日夜版) 申込みはこちら
4月18日(木) @港区勤労福祉会館
受付開始:18:30 セミナー開始:19:00 懇親会:21:15頃
大阪セミナー 申し込みはこちら
4月14日(日)@生涯学習センター梅田
受付開始:13:30 セミナー開始:14:00 懇親会:17:00
4月7日(日)タキプロ名古屋 春セミナーに道場メンバーがゲスト参加させて頂きます!名古屋近郊の方!是非、ご検討ください!
詳細はタキプロにて掲載中
❀:✿:❀:✿:❀:✿:❀:✿:❀:✿
どうも、kskn(きしけん)です。
桜がキレイな季節ですね。明日、東京メンバーはみんなで花見に行くそうです。そう、東京メンバーはね。(大阪在住)
また、今日は大阪で診断士青年部の例会なるものが開催され、僕もオブザーバーとして参加させていただきます。
少しずつ診断士としての活動が始まってきていて、とてもワクワクします!診断士、楽しいですよ。
そして来週は東京春セミナー、再来週は大阪春セミナーです。
僕は両方とも参加しますので、来られる方はぜひたくさんお話しましょう!
先日のタキプロブログでセミナーに関する記事を書きましたので、是非そちらを読んでセミナーへ臨んでください!→コチラ
では早速、今回も経済解説参ります。
今回は「効用、無差別曲線、需要関数、スルツキー分解」についてです。
これらは全て頻出の分野ですし、A~Cランクくらいの難易度に収まることが多いので絶対に取りたいところですね。
特に無差別曲線はいろいろなバリエーションで問題の出されるので、覚えようとせずに理解して臨みたい分野です。
※過去記事
第一回:費用関数
・効用、無差別曲線
まず言葉の説明からいきます。暗記する必要はありません。
効用とは「消費者がある財やサービスの消費によって得られる主観的な満足・欲望充足(への貢献)の度合いのこと」です。
ザックリ言い換えればその財やサービス(長いので今後は財とだけ書きます)を消費してどれくらい嬉しい気持ちになるかとか、どれくらいテンション上がるかとか、そういうことです。
また、どの財を消費してどれだけの効用が得られるかは人によって異なります。
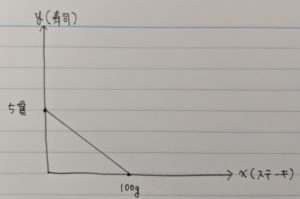
例えば僕は魚介類が好きで肉はそんなに好きじゃないので(知らんがな)、ステーキの効用は低く、寿司の効用は高いということです。
こうした効用の差は一般的には好き嫌いと言われますが、経済学ではこれを選好と言います。
そして、2つの財に対してそれぞれをいくつ消費したらどれだけの効用を得られるかを表す関数を効用関数と言い、同じ効用を得られる消費量の組み合わせを線で結んだ物を無差別曲線と言います。
と言っても分かりづらいと思うので、僕を例にとってお話しましょう。
上でもお話した通り、僕は肉より魚の方が好きなので、ステーキの効用は低く、お寿司の効用は高いです。
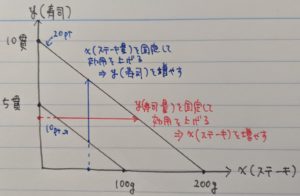
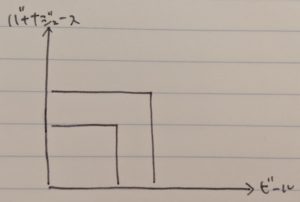
この効用を「嬉しいポイント」ととして、ステーキ10gにつき1嬉しいポイント(長いので今後は1ptとします)、寿司1貫につき2pt得られるとしましょう。
すると、10ptを得られるステーキの量と寿司の量の組み合わせを線で結ぶと下図のようになります。
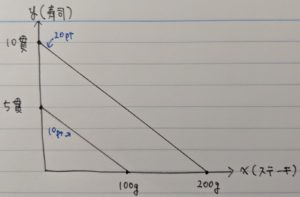
さらにこの図に20ptの無差別曲線を追加します。
寿司10貫は何とか食べれますが、ステーキ200gはちょっとキツいですね。。。
このように、ポイントが上がる=効用が高くなると、無差別曲線は右上へスライドし、原点から遠ざかります。
なぜこうなるかと言うと、例えばステーキの量を固定した状態で効用を高めようとすると寿司の量を増やすしかありませんし、逆に寿司の量を固定するとステーキの量を増やすしかないので、右上へとスライドするわけです。
また、このことから同時に異なる効用の無差別曲線は必ず交わらないということも言えます。
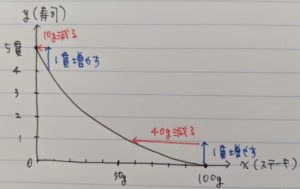
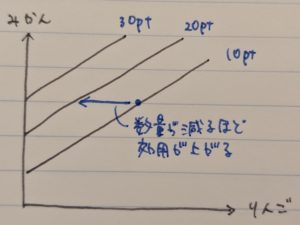
ところで、実際に寿司を食べる時を想像していただきたいのですが、1貫目を食べたときの嬉しさと5貫目を食べたときの嬉しさを比べると、5貫目の方が嬉しさは小さくなりませんか?
ご飯の一番の調味料は空腹とよく言いますが、やはり最初の一口は美味しく感じますよね。
となると、寿司を0貫→1貫に増やす時に増えるポイントは、4貫→5貫に増やす時よりも多いわけです。
例)
寿司を0貫から1貫に増やす → ステーキは100gから60gに減る (寿司0→1の効用はステーキ40g分の効用に等しい)
寿司を4貫から5貫に増やす → ステーキは10gから0gに減る (寿司4→5の効用はステーキ10g分の効用に等しい)
これを図示すると
となり、原点に向けて凸型のグラフになります。
このとき、寿司の量が増えるほどステーキに置き換える(代替させる)ときの量が減っていくので、限界代替率逓減であるということが分かります。(限界の言葉の定義は「第一回:費用関数」でやった通りです)
これが一般的な無差別曲線となります。
しかし、無差別曲線とは必ずこういう形になるかと言うとそうでもありません。そちらも例と一緒に考えてみましょう。
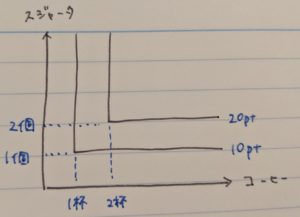
例1) ミルク入りのコーヒーしか飲めない
この場合、ブラックコーヒーだけをいくら消費しても効用は高まりませんし、スジャータだけをいくら消費しても(そんなやついるのか?)効用は高まりません。
ブラックコーヒーとスジャータを同時に消費してはじめて、効用が高まるというわけです。それを図示すると下図のようになります。
この図はつまり、コーヒーの量が1杯しかなければ、スジャータが2個あろうが3個あろうが効用は10ptから変化しませんし、反対にスジャータが1個しかなければコーヒーが2杯あろうが3杯あろうが効用は10ptのままということを意味し、コーヒーが2杯とスジャータが2個揃ってはじめて、効用は20ptへと高まることを示しています。
なお、こうした2財のことを完全補完財と言います。
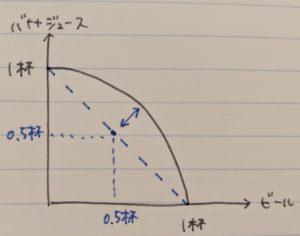
例2)バナナジュースとビールはそれぞれ好きだが、同時に消費するのは好きじゃない
この場合、バナナジュースを1杯だけ、もしくはビールを1杯だけ飲むより、両方を0.5杯ずつ同時に飲む方が効用が低いことになります。これを図示すると下図のようになります。
これでさらに、両方同時に飲むくらいなら片方捨てた方がマシ!というレベルになれば下図のようになります。
例3)みかんは好きだがりんごはどうでもいい
りんごが嫌いなわけではなくて、どうでもいいというところがミソですね。
この場合、りんごの個数は効用に影響を与えず、みかんの個数によってのみ効用が決まるので下図のようになります。
ちなみにもしりんごが嫌いだと、りんごの個数が減るほど効用が上がるので右上がりの直線になります。
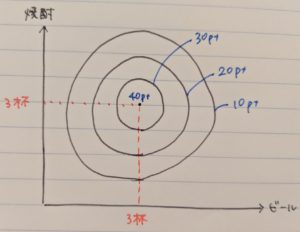
例4)ビールも焼酎も好きだが、特に3杯ずつ飲むと最も満足
飲み会の注文パターンが決まっているタイプですね。
この場合、ビール4杯と焼酎3杯でも、ビール3杯と焼酎2杯でも効用が下がってしまうわけですので、無差別曲線は下図のようになります。
無差別曲線の例をいくつか挙げましたが、これらあくまで一部でしかありません。全てのパターンを覚えるというのは無理だと思いますし、仮にできたとしても効率が悪いです。
無差別曲線で大事なのは「パターンの暗記」ではなく、「その無差別曲線がどういった状況を表現しているか」という本質的な部分です。この理解が十分にできていれば、本番でどのような形の無差別曲線が来ても対応できるでしょう。
過去問をいくつかご紹介します。
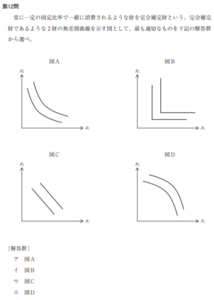
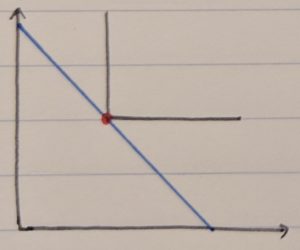
まずは平成27年度第12問。
これは知識問題ですが、万が一「完全補完財」という用語をド忘れしてしまったときにも問題文の頭にある「常に一定の固定比率で一緒に消費されるような財」から導きたいところです。答えはウ。
※3/31 訂正:コメントにてご指摘いただきました通り、答えはウではなくイです。。。確認不足スミマセン。。。
続いて平成29年度第12問。
これは上でも書いた通り、「興味がない=どうでもいい」がミソですね。答えはウです。ただこの問題に関しては、ぜひ他の選択肢がどういう形の無差別曲線になるかも考えてみてください。エは特に難しいと思います。
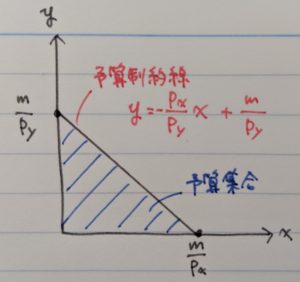
・予算制約線
ここまで書いたように、効用関数にはいろいろなパターンはあるのですが、全てに共通して言えることは効用とは基本的に「財を消費して得られる」ので、つまり「お金がかかる」ということです。
なので、その消費にいくらお金を使えるか、つまり予算によって制約を受けるわけです。この予算による制約を図で示した線を予算制約線、そして予算制約線より下の範囲(予算の範囲内に収まるエリア)のことを予算集合と言います。
グラフには予算制約線の式を書き込みましたが、特に覚える必要はありません。一般式から導出できる方はそれで十分ですし、難しい方は下記の例を参考にしてみてください。
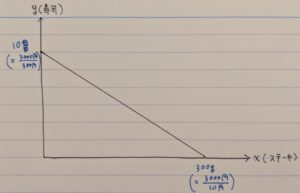
最初の寿司とステーキを例として考えてみましょう。
仮に予算は3000円、寿司は1貫=300円でステーキは1g=10円とすると、寿司は3000円/300円=10貫が最大消費量、ステーキは3000円/10円=300gが最大消費量であると分かります。これをグラフで表すと下図の通りです。
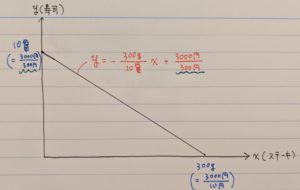
そしてこの図から予算制約線の式を導こうとすると、Xが300g増える間にYは10貫減るので傾きは300g/(-10貫)となり
となります。ここでX財、Y財の単価を見ていただきたいのですが、Px=10円、Py=300円ですから、傾きは-Py/Pxとも等しいということが言えるわけです。
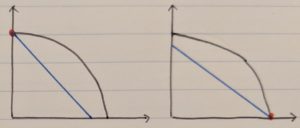
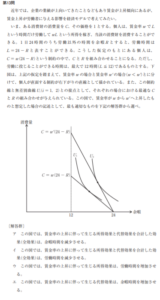
そして、このような予算の制約の中で、最も効用が大きくなる点を最適消費点と言い、これは無差別曲線の形によって変化します。
例えば一般的な凸型のグラフでは無差別曲線と予算制約線の接点になりますし、
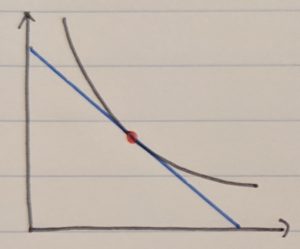
円型であれば、予算集合内に中心点があれば中心点。予算集合外に中心点があれば円と予算制約線の接点になります。
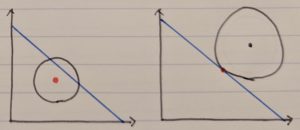
円型はかなり特殊なので例外的ですが、それ以外は基本的に「消費量を増やす→効用が上がる」が成り立つケースが多いので、そうである場合は最適消費点は必ず予算制約線上に存在するということも言えます。(予算制約線は予算の限界なので、予算制約線上でない点はまだ消費を増やす余地があるということ)
それではここでも過去問を見てみましょう。
まずは平成27年度第14問。
ア→最適消費点は予算制約線と無差別曲線の接点なので、これ以上に効用の上がる余地はありません。よって誤り。
イ→問題文にもある通り財X1の単価は2なので、財X1だけで所得80を使い切るために必要な消費量は40ですね。よって誤り。ちなみにこれはグラフで言うとbの値になります。
ウ→aの値は、所得:80/財X2単価:4=20なので、財X1の単価とは無関係です。よって誤り。
エ→問題文に、効用関数U=X1(の消費量)×X2(の消費量)と書かれています。図中の無差別曲線Uは最適消費点(X1, X2)=(20, 10)を通るのでU=20×10=200となり、この無差別曲線上は全て効用が一定なので正しいと言えます。
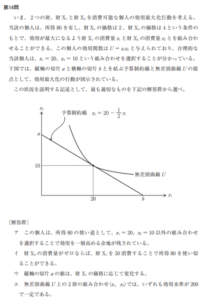
続いて平成25年度第13問。
これは正直解けなくてもいい問題だと思います。まずそもそも設問の意味が分かりづらいので、本番でこういう問題が来たらとりあえず飛ばした方がいいですが、いちおう説明します。
少し話を具体化するために、若年期(期間1)を21~40歳までの期間、老年期(期間2)を41~60歳までの期間とします。
そして問題文に「期間 i (i = 1,2) における消費を Ci、所所得を Yi」とありますが、これはつまり、21~40歳の間(期間1)の総所得をY1、41~60歳の間(期間2)の総所得をY2ということで、Y1の点は期間1で得た収入は期間1のうちに全部消費しますよ、ということです。
「じゃあAとBって何やの?」という話なんですが、点Aは「期間1で得た所得(Y1)を1円も使わず、全て貯蓄に回した後、期間2で消費した」ときの消費量というわけです。また点Bは逆に「期間1の間に、期間2の所得(Y2)分までも先食いして消費した(つまり今の所得(Y1)では足りず、借金をして消費に回した)」ときの消費量というわけです。そして貯蓄ないし借金をした場合にはその分に利子が付くのは当然ですね。
となると点Aは期間1から持ち越したY1分にのみ利子が付くのでY2+(1+r)Y1、点Bは借りたお金に利子がついてY2となるのでY1+Y2/(1+r)となるわけです。
ここまで分かれば傾きはOA/OBで求められますので、計算は省略しますが1+rとなります。よって答えはウ。
・スルツキー分解(と需要関数)
スルツキー分解は、所得もしくは財の価格が変化することで予算制約線も変化し、それに伴う最適消費点のシフトを所得効果と代替効果の2要素に分解することを言います。そしてこれをすることでその財が上級財ないし下級財(もしくはそれ以外)であることを調べることができます。
これらの分野についてはテキスト以上に語れることがないので過去問中心に解説していきます。
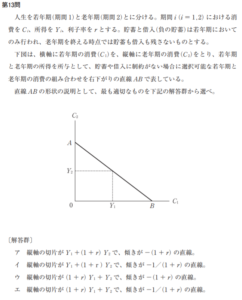
まず平成26年度第16問。
最適消費点の移動について改めておさらいですが、点L→(代替効果)→点M→(所得効果)→点Nと移動していきます。
このときの各財の消費量を見ると、財Xは代替効果、所得効果ともに増加。財Yは代替効果で減少、所得効果で増加していることが分かります。つまり両財ともに上級財であると言えます。
これらの内容から、正しい答えはエとなりますね。
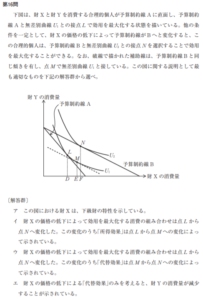
続いて平成27年度第13問。
これも設問が変わっているので少し難しく見えますが、ただのスルツキー分解と思えば大したことない問題です。
ア→最適消費点は右に移動し余暇時間は増加しているので誤り。
イ→アより余暇時間が増加しているので、反対に労働時間は減少する。よって正しい。
ウ、エは補助線を引いて確認すればすぐに分かりますので説明は省略します。
まぁスルツキー分解自体はそこまで理解に苦労することも少ないと思いますし、試験を出す側として考えてもなかなか難しい問題が作り辛そうなので、用語をキチンと把握して確実に取りたいところですね。
さて、いかがでしたでしょうか。
今回もなかなかなボリュームになりましたね。。。
分からない箇所があれば、コメントで質問を受け付けておりますのでぜひお願いします。
ではでは、引き続き勉強頑張ってください!
(=゚ω゚)ノホナ、マタ!!




さっと書いたようなグラフが美しすぎて、内容もすっと入ってきました!
このグラフが自分で描けるようになったら合格する気がする…‼︎
苦手分野だけに解説ありがたいです、ksknさん大好きです!
きういさん
コメントありがとうございます!
そのようなお褒めの言葉をいただけて感激です…!
今後も引き続き経済の解説を書いていきますので、ご贔屓によろしくお願いいたします。
>両方同時に飲むくらいなら片方捨てた方がマシ!というレベルになれば下図のようになります。
→その図ですが直線で描かれているという解釈でよろしいでしょうか。限りなく直線に近いが(原点に対して凹型の)曲線であるというならば代替性を満たしますが、水平垂直な直線ならばそこが否定されると考えます。そして、先に説明いただいた完全補完財でもなく直後の独立財とも違うとなりますと、いままで触れたことがなかったもので確認させていただきました。いずれにしても最適消費点はコーナー解だから深入りするなと言われそうですが、どうしても気になったものですみません。
あと、書き間違いだとは思いますが平成27年度第12問の正答はイですかね。ウは完全代替財です。
KKKさん
コメントありがとうございます。
ご指摘いただいた図について、このような問題を見たような記憶があったので書いたのですが、直線は適切でないかもしれないです。
ただイメージとしては、単独で好きな食べ物でも食い合わせが絶望的に悪くて同時に食べるならどちらかを1つだけ食べた方がマシということは現実的にあると思います。そうなると、(消費という言葉の定義にもよるのですが)廃棄することも(財が無くなるという意味で)消費であると考えれば、単独での効用が高い方の財数量が2財における効用の高さを律するということになるので、こういうグラフも有り得なくはないのかなと思っています。(答えになっていませんが 笑)
平成27年度第12問に関してはご指摘いただいた通り、誤っておりましたので訂正いたしました。ありがとうございます。