【独学者向け】経済学解説①「費用関数」
✿:❀道場 春セミナー受付中✿:❀
東京セミナー 申し込みはこちらから
4月6日(土) @港区勤労福祉会館
受付開始:13:30 セミナー開始:14:00 懇親会:17:00
東京セミナー(平日夜版) 申込み受付3月24日(日)12時開始
4月18日(木) @港区勤労福祉会館
受付開始:18:30 セミナー開始:19:00 懇親会:21:15頃
大阪セミナー 申し込みはこちらから
4月14日(日)@生涯学習センター梅田
受付開始:13:30 セミナー開始:14:00 懇親会:17:00
4月7日(日)タキプロ名古屋 春セミナーに道場メンバーがゲスト参加させて頂きます!名古屋近郊の方!是非、ご検討ください!
詳細はタキプロにて掲載中
❀:✿:❀:✿:❀:✿:❀:✿:❀:✿
どうも、kskn(きしけん)です。
さてさて、最初にお知らせですが、おそらく一発合格道場では初となる、平日夜の春セミナー(@東京)を開催します!!
(パチパチパチ!)
日時は、4月18日(木)19時開始、場所は、田町駅の港区勤労福祉会館を予定しています。
通常の春セミナーは土日開催なので、「土日だと、仕事or家族サービス等で行けないよ~」という方に是非来てもらいたいな、ということで今回企画いたしました。
内容は、通常の春セミナーとほぼ同じ、①セミナー(通常の春セミナーと同じ内容ですが、少し短縮版)、②個別相談会、③懇親会(希望者のみ)を予定しています。
ただし、一発合格道場でも初めての試みで、どれくらい読者の皆様に来ていただけるか全く不明ですので、あまりに参加者が少なければ中止ということもありえます。
土日の春セミナーに行けないという方は、ふるってお申し込みください!
申込み開始は、こくちーずにて、3月24日(日)12時~を予定しています!
(詳細は、上記テンプレ参照)
次に他団体のお知らせですが、タキプロでもブログを書かせていただくことになりました!(こちら)
道場では学習法や解説などの技術(?)面、タキプロではモチベに繋がりそうな精神(?)面などを書いていけたらいいなと思っています。
さらに、タキプロも春セミナーを開催いたしますので合わせて宣伝させてください!
東京は3/21、大阪は4/6、名古屋は4/7です。詳しくはコチラへ!ちなみに大阪セミナーはまだ少し席に余裕があるそうです。皆さんぜひぜひご参加ください!
また、東京ではすでに二次試験向けの勉強会もスタートしています。大阪は5月からスタートです。僕もなるべく参加するつもりなのでそちらもぜひお越しください!
では他団体の宣伝も終わったところで(笑)、タイトルにもあります通り、今週から経済学の解説記事を書いていきます。
経済学は二次試験とも関連がありませんし、わりと暗記で対応できる部分もあるので時間をかけて深く理解しようという方は少ないかもしれません。
しかし、経済学は政治や実社会との関連が強い学問ですので、経済学の理解が増すことでニュース等に対してより深い考察ができるようになります。例えばこちら。
こうして様々なことに対して考察を重ね、考える癖を付けるということは必ず二次試験にも活きるはずです(ブブさんも仰ってましたね!)ので、経済学への理解がその1つのキッカケとなればいいなと思っています。
解説はなるべく詳しく書きたいと思っていますが、説明が長くなりすぎるのもよくないので一部省略する部分があります。もし分かりづらければ補足しますので、遠慮なくご質問ください。もし説明が間違っていると思った際も、お手数ですがご指摘いただけると幸いです。また、解説を読み始める前にきゃっしぃさんの記事を一読されることをオススメいたします。
それでは、第1回は費用関数からいきます。
なお、参考資料としてTACのスピードテキストを使用しております。また、記事に出てくる画像はクリックすると拡大できますので、ご参照ください。
・固定費用と可変費用
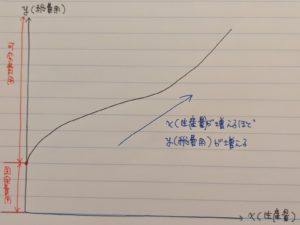
まず、費用関数とは下図のようなグラフのことですね。
これは生産にかかる費用を表したグラフで、横軸(X)は「生産量」、縦軸(Y)は「総費用」を示しています。グラフは右に行くほどXの値が大きくなることを示しているので、「生産量が増えると総費用も増えていく」ということが分かりますね。
また、総費用はグラフの左側に書いた、固定費用と可変費用に分けられます。
固定費用→生産量に依存しない費用
可変費用→生産量に依存し、変化する費用
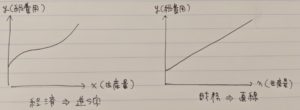
これは財務の固定費・変動費の考え方と全く同じで大丈夫です。ただ一点異なっているのは、財務における費用関数は直線(一次関数)的なグラフになりますが、経済における費用関数は逆S字型の曲線(三次関数)となります。なぜ同じ物であるはずなのに異なるグラフになっているかはそんなに深い意味はないのでスルーしてください。問題が作りやすいからという理解でいいと思います。
また、上で財務のグラフは一次関数、経済のグラフは三次関数と書きました。これを数式で表すと
財務:Y=cX+d
経済:Y=aX3+bX2+cX+d
(a,b,c,dは全て定数)
となります。
さて、それぞれのグラフの可変費用部分と固定費用部分は分かりますか?
ここで一旦、言葉の定義に戻ります。
固定費用→生産量に依存しない費用
可変費用→生産量に依存し、変化する費用
そして、グラフにおいて生産量は横軸(X)で示しています。これにより、下記のように言い換えることができます。
固定費用→生産量に依存しない費用→Xによる影響を受けない部分
可変費用→生産量に依存し、変化する費用→Xによる影響を受ける部分
つまり、費用関数@経済において可変費用はaX3+bX2+cX(→Xが入っている部分)、固定費用はd(→Xが入っていない部分)というわけですね。
ちなみにこの固定費用dは、X=0のときのYの値に同じ(Y=a×03+b×02+c×0+d=d)ですので、費用曲線とY軸の交点(これをY切片と言います)が固定費用を示すということが分かります。
(なお、費用関数@財務における可変費用はcX、固定費用はdです)
・平均費用と限界費用
ここでは本題に入る前に、知識の確認をしましょう。
5人でいちご狩りに行って、合計で100個のいちごを収穫しました。5人は平均何個収穫したでしょう?
答えは100÷5=20(個)ですね。問題ないでしょう。
少し本題に近づけます。
テレビを10,000台生産するにあたって、費用が200,000,000円かかりました。平均費用はいくらでしょう?
答えは200,000,000÷10,000=20,000(円)です。これも大丈夫でしょう。
では、費用関数における平均費用を求めてください。
どうでしょうか?ここでつまづいてしまった方は、きっと数式を難しく考え過ぎだと思います。もっとシンプルに考えましょう!
平均とは「合計÷数量」であり、また費用関数はX個作ったときの総費用がY円になるよということですから、平均費用(AC)は
となります。(Y= aX3+bX2+cX+dより)
平均可変費用(AVC)も求め方は同じですね。可変費用部分のaX3+bX2+cXを個数Xで割って、
となります。
そして、これらがグラフで何を表すかというと、
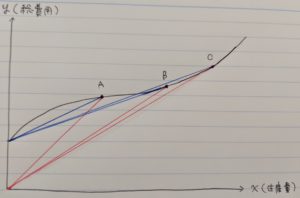
平均費用は任意の(=点A, B, Cみたいにどこでもいいから適当な)点における、原点と費用曲線を結んだ直線(赤線)の傾き
平均可変費用は任意のXにおける、Y切片(=固定費用)と費用曲線を結んだ直線(青線)の傾きを表すのです。
次に限界費用の説明に移ります。
まずそもそも限界費用とは何かと言うと、「生産を1単位増加したときの総費用の増加分」だそうです。そしてこれは費用関数を微分することで求まります。
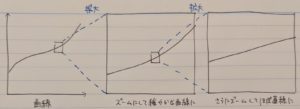
これをもう少し詳しく説明すると、微分とは「曲線になってるグラフでもめっちゃズームにして小さな点で見たらほとんど直線に見えるから、その傾きを求めればその点での『生産を1単位増加したときの総費用の増加分』が分かるよね」っていう物なんです。何となく分かっていただけますかね。グラフをめっちゃ細かくするから、微分です。覚えやすい。
また、微分して得られた直線は、その点における接線と等しいという特徴があります。

(赤線は微分して得られた直線。費用曲線の接線になっていることが分かる)
つまり、費用曲線上のある点における限界費用とは微分を用いて求められ、それはその点における接線の傾きと等しいということです。
そして、Y=aX3+bX2+cX+dを微分すると、Y’=3aX2+2bX+cとなります。(なぜこうなるかの説明は割愛します。興味あれば質問してください)
※余談ですが、経済学の中で「限界〇〇」となっているものは全て同じように微分することで求められます。限界生産性とか限界効用とか。
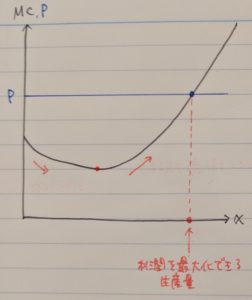
さて、ここでもう一度費用曲線に戻りたいのですが、様々な点における接線の傾きを考えると、下左図より生産数量の少ない時は傾きが急(①)→緩やかになる(②)→ある点を境に再度急になる(③)ということが分かると思います。この限界費用(MC)の変化をグラフで表すと、下右図のようになります。傾きが緩やかになる=MCが小さくなる、傾きが急になる=MCが大きくなるということから、MCのグラフは下に凸になることが分かります。
もう秒殺ですね。特に解説もしません。
・利潤最大化行動
ここはテキストの説明が分かりやすいので詳しくは割愛しますが、企業は「価格=限界費用」となるように生産量を決定します。例えば費用関数がY=aX3+bX2+cX+d、価格が1つあたり100円だとすると、3aX2+2bX+c=100を満たすX個生産します。上で述べたように限界費用は費用関数の接線の傾きを表しますので、収入を示す直線と接線が平行となるような点Xが利潤を最大化できる生産量ということになります。
また、上で示した限界費用のグラフに価格を追加すると下図の様になります。繰り返しますが、限界費用の値は費用関数の接線の傾きを示していますので、接線と価格が平行になる=限界費用と価格が等しくなる点が利潤を最大化できる生産量となります。
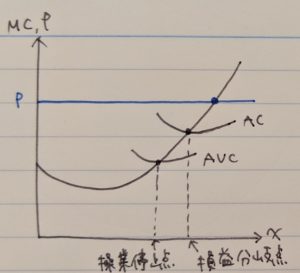
・損益分岐点と操業停止点
まず言葉の説明からいきましょう。
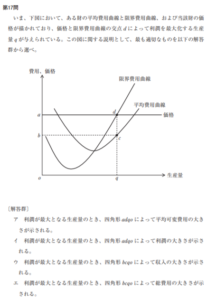
益分岐点→総費用と総収入が一致する点(それより費用が増えると損、収入が増えると益が出る点)。言い換えると、平均費用と価格が一致する点。
操業停止点→可変費用の合計と総収入が一致する点(それより収入が増えると固定費用はいくらか回収できるので操業しても良いが、費用が増えると回収できないので操業すべきでない)。言い換えると、平均可変費用と価格が一致する点。
ここに前項の利潤最大化行動より、企業は価格=限界費用となるように生産量を決定するということが分かっているので、
損益分岐点→平均費用と価格が一致する点。すなわち、平均費用と限界費用が一致する点
操業停止点→平均可変費用と価格が一致する点。すなわち、平均可変費用と限界費用が一致する点
と言い換えることもできます。
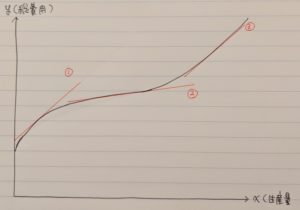
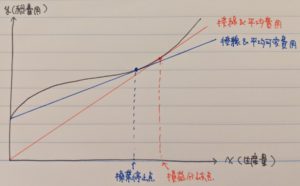
これをグラフで表すと下図のようになります。
さて、このグラフは損益分岐点と操業停止点を示したグラフですが、このグラフより、「赤線、青線より傾きの緩やかな直線は費用関数と交わらない」ということも分かります。
このことから何が言えるかと言うと、
①平均(可変)費用=限界利益となる点は、平均(可変)費用の最も小さな値となる。
②生産量(X)が損益分岐点(操業停止点)から変化すると、平均(可変)費用は必ず増加する。
という2つのことが言え、これらと損益分岐点(操業停止点)では平均(可変)費用=限界費用となることから、平均費用と平均可変費用をグラフにすると「どちらも下に凸のグラフとなり、最下点(最も小さな値)で限界利益と交わる」ということが分かります。(※ここは少し理解が難しいかもしれません。分かりづらければ暗記でもいいと思います。おそらく深く問われることはないと思うので)
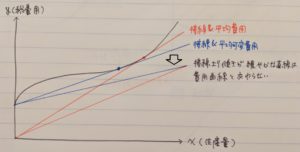
ちなみにこれをグラフで表すと下図のようになります。
また、このグラフは最適な生産量が損益分岐点を上回っているので利潤を得られる状態にありますが、損益分岐点を下回るパターンと操業停止点を下回るパターンのグラフは下の2図となります。
・最適な生産量が損益分岐点を下回るが、操業停止点を上回っているので固定費の回収はできている状態
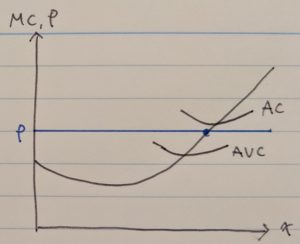
・最適な生産数量が操業停止点を下回っているので、作れば作るほど損失が拡大していく状態
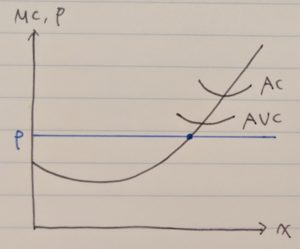
最後に、試験問題ではこのグラフを用いて、利潤総額や固定費用総額、可変費用総額がどの部分に相当するかを問われることがあります。
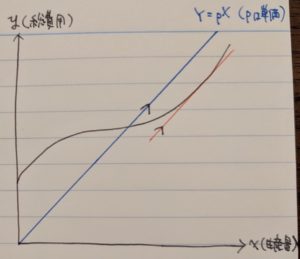
これを、仮に最適な生産量をX*(X*>損益分岐点)、価格をpとしてグラフに示したのが下図です。
これを順を追って説明していくと、
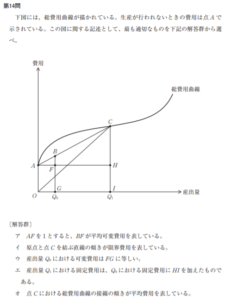
まず、可変費用総額=平均可変費用(生産量X*におけるAVC)×生産量(X*)(※平均×数量=合計より)となり、下側の赤四角を表していることが分かります。(※AVCの値を縦、X*を横とした四角形の面積を求める計算と同じなので)
また、費用総額も同様に費用総額=平均費用(生産量X*におけるAC)×生産量(X*)となり、これは赤四角全体を表しています。
そうなると、固定費用総額=費用総額-可変費用総額となることから、赤四角全体から可変費用総額分を除いた部分(上側の赤四角)が固定費用総額を表すこととなります。
また、四角全体は売上総額(=価格(p)×生産量(X*))を表しているので、売上総額(四角全体)から費用総額(赤四角全体)を除いた青四角部分が利潤総額を表すこととなります。
ここはぜひ、pが変化して損益分岐点や操業停止点を下回ったケースも考えてみてください。
すぐ上で説明した通りです。秒殺ですね。
これも説明した通りですね。
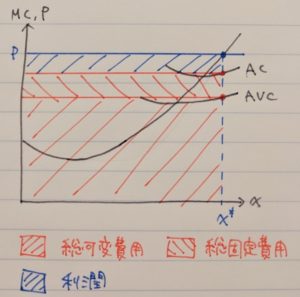
ア→グラフから平均可変費用はCH/AHとなるわけですが、△ACHと△ABFは相似(形は同じだけど大きさが違う)関係にあるので、CH/AH=BF/AFが言えます。この中のAFが1ということなのでBF/1=BFとなり、正しいことが言えます。
イ→原点と点Cを結ぶ直線の傾きは平均費用ですので誤り。
ウ→FGは固定費用なので誤りですね。なお蛇足ですが、生産量がQ0のときの総費用は、線BGを更に上に伸ばし、総費用曲線と交わる点(仮に点Jとします)と点Gの長さとなります。総費用がJG、固定費用がFGなので可変費用はJG-FG=JFとなります。
エ→固定費用は生産量に依存しないので、Q1であってもFG(=HI)です。選択肢の内容は、固定費用=FG+HIということを言っていますので誤りです。
オ→これは一瞬引っ掛かりそうになりますが、点Cにおける平均費用は線OCの傾きを示していますが、線OCが接線であるかどうかは分かりませんので誤りです。もし、「点Cが損益分岐点である」という記述が問題文にあった場合は、損益分岐点の条件より線OCが点Cの接線と等しいということが言えるので、正しい選択肢となります。
最後に平成30年第19問。
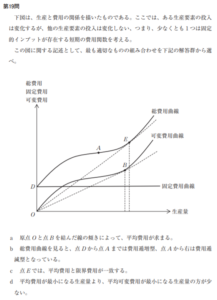
これは総費用曲線と可変費用曲線が別々に書かれているので何となくややこしい感じがしますね。
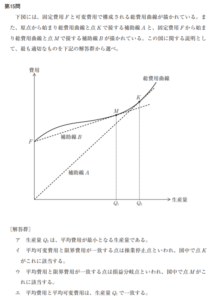
a→平均費用は原点Oと点Eを結んだ線の傾きなので誤りですね。線OBの傾きは平均可変費用を表しています。
b→費用逓増型は接線の傾きが徐々に急=限界費用が徐々に増加、費用逓減型は接線の傾きが徐々に緩やか=限界費用が徐々に減少となります。しかし費用関数は下図の様に、限界費用が減少→増加へと切り替わりますので、点Aまでは費用逓減→点A以降は費用逓増となり、選択肢とは逆になります。ですので誤り。
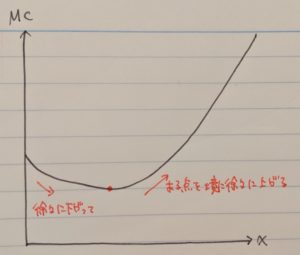
c→線OEが費用曲線の接線であるという記述がないので微妙なところですが、a,bが明らかに誤りなので消去法で正しいとしましょう。まぁグラフでは接線っぽく見えるのでセーフということで。個人的には条件記述が甘いのであまり良い選択肢ではないと思います。
d→これは必ずこうなりますので正しいです(説明は長くなるので割愛します。興味があれば聞いてください)。これは言い換えると、「損益分岐点より操業停止点の方が生産量が少ない」ということが必ず成り立つということにもなりますのでこれも覚えておきましょう。
さて、費用関数についての解説は以上となります。数学が苦手な方には少し難しい内容だったかもしれませんが、もし分からない部分があれば遠慮なくコメントにてご質問ください!
このセクションが十分に理解できていれば、生産関数もグラフの形が違うだけで理解の仕方は全く同じだから問題ないと思います。
また、次回以降も大事そうなセクションだけに絞って説明をしていくつもりですが、もしこの範囲をやってほしいという希望があればリクエストお願いいたします。
次回は効用関数とスルツキー分解、それで書く文量が少なければ需要と供給、余剰分析あたりまでいくかもしれませんので、お楽しみに!
PS. Twitterを再開したのでよければフォローお願いします! https://twitter.com/kskn41
(=゚ω゚)ノホナ、マタ!!

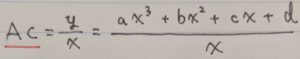
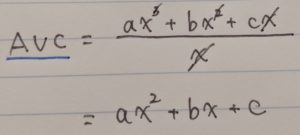


少ない知識でいろいろな問題に対処できますね。
こういう解説好きです。
>生産関数の乗数が1以上、1以下の時にそれぞれどういうグラフになるか
→問題として扱われる生産関数のほとんどが1次同次関数つまり規模に関して収穫不変で議論されている認識でいました。私の課題はその先の例えばオイラーの定理を使って乗数の意味を確認するあたりにあったのですが、ポイントはその前でしたか。改めて見直してみます。ありがとうございました。
KKKさん
やりとりさせていただいている中で、まだあまり問題集や過去問での演習には取り組まれてらっしゃらないのかなとお見受けいたしました。(間違っていたらすみません)
KKKさんは高い数学の素養をお持ちだと感じますが、診断士試験を受ける受験生の大半はそうではない(数ⅢCまでやっていないという意味です)ので、試験に求められる数学レベルはそれほど高くありません。
あまり深掘りしすぎたところで点数に繋がらないので、演習をしながら難易度に合った学習をされることをオススメいたします。
早速のご回答ありがとうございます。
①費用関数の仮定によって利潤最大化の議論の仕方も変わるが、その仮定部分はあまり気にするなと。そのようにします。
②微分して傾きが得られ元の関数と接する直線ということですね。そしてその傾きがこの場合は生産量xの2次関数であると。よくわかりました。
③コブダグラス型をやっているうちによく分からなくなってきたのですが、例題となりますと改めて質問したいと思います。そのときはよろしくお願いします。
引き続き楽しみにしております。
KKKさん
①仰る通りです。そもそも利潤最大化行動自体も仮定ですので、その仮定を説明するためにした更なる仮定を深追いしてもしょうがないだろというのが僕の考えです。
②仰る通りです。理解いただけたようで良かったです!
③生産関数については、それぞれの言葉の定義と、生産関数の乗数が1以上、1以下の時にそれぞれどういうグラフになるかが分かっていれば問題ないと思います。もし問題があれば、いつでもご説明しますので遠慮なくご連絡ください^^
>財務における費用関数は直線(一次関数)的なグラフになりますが・・・問題が作りやすいからという理解でいいと思います。
→規模の経済といったあたりの話と理解していましたが「深い意味はない」となりますと誤っていますでしょうか。
>(限界費用の説明にある)微分して得られた直線
→どの関数を微分するとその直線が得られるのかお願いします。総費用関数を微分しても放物線しか得られないと思ったもので。
>生産関数もグラフの形が違うだけで理解の仕方は全く同じ・・・リクエストお願いいたします。
→生産関数がよく分かりませんのでリクエストしたいです、よろしくお願いします。
KKKさん
コメントいただきありがとうございます。以下3件、解答いたしますね。
①グラフの形について→仰る通り、規模の経済などが関係する部分ではあります。が、経済学や財務会計における費用のグラフはそれぞれ三次関数、一次関数となるように学問上「仮定」されたものでしかありません。現実世界での費用関数はおそらく逆S型となるものが多いと思うのですが、鉄道や水道などのインフラ業界は費用逓減産業と呼ばれ逆S字にはならないものもありますので、あまり深く考えず「そういうもんだ」と思った方が良いです。イメージとしての捉え方は正しいです!
②微分について→限界費用は総費用関数の微分です。一度、微分の導出から考えていただけると分かりやすいと思いますが、微分はそれが何次関数であろうが、あくまで接線の傾きを求めることしかできません。
KKKさんが仰られているのは、「三次関数を微分すると二次関数が得られる」ということだと思いますが、この二次関数はあくまで三次関数の各点の「傾きの集合体(X=1,2,3,…のときの各点における接線を一般式化したもの)」であり、この集合体が二次関数になるので記事中盤にあるMCのグラフは下に凸の放物線となります。(分かりづらい説明ですね。。。すみません)
③生産関数について→生産要素や平均生産物、限界生産性などは費用関数と全く同じアプローチで大丈夫ですよ。過去に解けなかった例題などあれば、それについて解説いたしますのでお手数ですが教えていただけますか?ブログのコメントには画像が貼れないと思いますので、Twitterか、もしくはippatsugoukaku10th@gmail.com宛にメールいただければお返事いたします!(②の説明も上記で分からなければそちらで図を用いて詳しく説明いたします!)