【経済学】 3.グラフ対策part2
こんにちは、 Xレイ です。
今日は、経済学のグラフ対策part2。
『消費者行動の理論』をみていきます。
消費者行動の理論
何らかの形で毎年1~3問出題されている、予算制約線・効用・無差別曲線関連、代替効果・所得効果等の領域です。
この領域は、例えば『2財の消費量(x,y)と効用(u)の関係』というような3次元関数を多く扱います。
数式があまり出てこないのは幸いですが、グラフにしても、3変数の扱いは通常慣れていないところです。
表現が難しいのですが、より幾何的にといいますか、ビジュアル的にといいますか、『右へ左へ』といったような捉え方が有効と感じています。
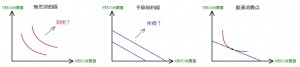
1.無差別曲線 予算制約線 最適消費点
2.代替効果 所得効果 (スルツキー分解)
3.上級財 中立財 下級財 ギッフェン財
まずは基本的な概念の確認です。
グラフ問題全般にいえるのですが、『基本的な知識を基に考えて解く』
といった対応が求められるでしょう。
前向きに捉えると、『考える余地のある問題』ということです。
多少難しくされても、全く知らない知識を問われるよりはマシです。
その正答率を高めるために、基本的な知識をしっかりと身に付けて臨みたいところです。
4.特殊な無差別曲線
5.応用論点
後半は、この領域の難しそうなところをみていきます。
深入りしていますので、必要なければ軽く流してください。
1.無差別曲線 予算制約線 最適消費点
・一般的な無差別曲線
①右下がり(単調性の仮定)
②原点に凸(限界代替率逓減の仮定)
③交わらない(推移律の仮定)
④右上にあるほど効用が高い(不飽和の仮定)
・予算制約線
①傾きの絶対値=財の価格比
②所得が増加すると右上に移動する(切片の値が上昇する)
・最適消費点
①予算制約線と無差別曲線が接する点
②最適消費点では 限界代替率=財の価格比
まずは、基本事項の整理です。
一通りその意味するところを知った後は、すべての文言を覚えるのではなく、グラフでイメージできるようにすることが実践的といえるでしょう。
2.代替効果 所得効果 (スルツキー分解)
【出題~H26問16 H25問14 H24問17 H20問18 H19問16】
設問では、代替効果・所得効果の識別が繰り返し問われています。
スルツキー分解を以下の程度知っていれば、ほとんど対応できるはずです。
〔スルツキー分解〕
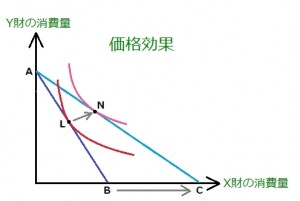
上はX財の価格の低下によって、予算制約線がABからACへ、
それに伴い、最適消費点が点Lから点Nへ変化したところです。
この変化は『価格効果』と呼ばれ、以下の2つの要素からなっています。
(価格効果は、全効果・全部効果とも呼ばれます)
X財の価格が低下したことによって
①Y財と比べて相対的にX財が安くになった
②実質的な予算(所得)が増加した
①による変化が『代替効果』、②による変化が『所得効果』です。
つまり、価格効果は代替効果と所得効果に分解され
『価格効果』=『代替効果』+『所得効果』 と表せます。
これが、スルツキー分解です。
それでは、各々効果の程を調べてみましょう。
いま、価格効果は分かっているので、あと一つ分かれば引き算です。
そこで、代替効果を求めてみます。
『代替効果』とは何なのか。先ほどよりも詳しく言うと、
『財の価格比が変化したときに、いまと同じ効用を得る』ための消費量の変化です。(少し難しく、補償需要を求める変化といえます)
さて上のグラフに戻って、
確かに価格比(予算制約線青→水色)は変化しています。
しかし、効用(無差別曲線赤→ピンク)も変化してしまっています。
そこで、価格比(傾き)は変化後のままにして、効用は変化前と同じ状態に戻してみましょう。そうすると、代替効果が分かるはずです。
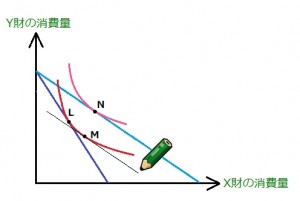
それをグラフで行うと、
変化後の予算制約線と平行な直線を(価格比は変化後のまま)
変化前の無差別曲線と接するように引く(効用は変化前と同じ)
ということになります。
(設問では、およそこの状態のグラフから問いかけられます)
そして、当初の点Lから点Mへの変化こそが『代替効果』。
あとは 『価格効果』=『代替効果 』+『所得効果』なので、
効用の大きさを変化させている点Nへの残りの変化
すなわち、点Mから点Nへの変化が『所得効果』となるわけです。
そこから、必要に応じて2財各々の消費量の変化を
X財であれば横軸 Y財であれば縦軸 に着目し、
それぞれの点から読み取ります。
設問では、例えば
〔ア.代替効果によって点Lから点Mへ変化した〕
のように、2財同時の変化を表した選択肢と
〔イ.代替効果によってX財の消費量は増加した〕
のような、どちらか一方の変化を表した選択肢を混在させてきます。
各々選択肢に合わせてグラフから読み取り、正誤を判断します。
・・・・・・・
以上、X財の価格低下の局面でみてきました。
他にもX財の価格上昇、Y財の価格低下・価格上昇のパターンがあります。
各々に、多少は慣れておくことが望ましいでしょう。
そうでなければ、試験本番で混乱する恐れがあります。
例えば、以下の 3.で説明する『財の分類』を、価格上昇局面では
所得の減少による消費の変化で行わなければいけません。
①『価格効果』= 『代替効果』+『所得効果』
② 代替効果 価格比~変化 効用~不変
③ 所得効果 価格比~不変 効用~変化
3.上級財 中立財 下級財 ギッフェン財
【出題~H26問16 H24問17 H23問19】
〔ウ.X財は上級財の性質を示している〕
というように、これらも上記設問の選択肢に混ぜてきます。
上級財~所得の増加によって消費が増える
中立財~所得の変化によらず消費は一定
下級財~所得の増加によって消費が減る
これらは、所得の変化による消費の動向で分類されます。
よって、スルツキー分解のグラフでは『所得効果』のみを考えます。
また、ここでの財の分類は、X財とY財の各々に与えられる性質なので、
必要などちらか一方に着目をします。
引き続き、X財の価格低下局面(実質所得増加の局面)でみてみましょう。
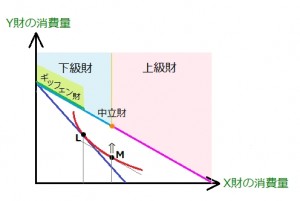
それでは、X財について調べてみます。
いま、代替効果によって点Lから点Mへ変化したところです。
ここから、『所得効果』によるX財の消費の増減(X軸の値の変化)
すなわち 『点Mから左右どっちの方へ行くのか』をみます。
移動する距離(高さ)は関係ありません。向かう方向が重要です。
その行く方向によって
ピンクの線上~上級財
境界の橙点 ~中立財
水色の線上 ~下級財
となります。そして
緑の線上 ~ギッフェン財
ギッフェン財とは、価格の変化による消費の動向で分類される財です。
すなわち、『価格効果』による消費の増減をみます。
この例でいうと点Lよりもさらに左へ、つまり価格が低下すると消費が減少してしまう財のことです。そうなるためには
① 下級財
②『代替効果』<『所得効果』
以上、2つの条件を同時に満たさなければいけません。
平成23年問19では、そのことを直接問われました。
①上級財・中立財・下級財は、所得と消費の変化で分類
②ギッフェン財は、価格と消費の変化で分類
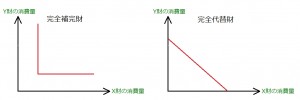
4.特殊な無差別曲線
【出題~H24問16 H23問16】
完全補完財(レオンチェフ型選好) と 完全代替財。
過去に一度ずつ出題されていますが、いずれまた出てくる気がします。
そのときは、最適消費点を問われるでしょうか。
可能性が高いのは、完全代替財の方(図右)。
予算制約線と無差別曲線(直線)の傾きが異なる場合、
最適消費点は、必ずX切片もしくはY切片に(端点解・コーナー解)、
また、傾きが同じ場合は、予算制約線上のすべての点が最適となります。
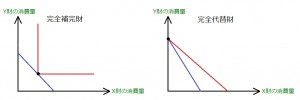
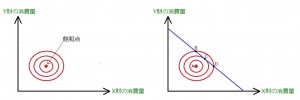
もう一つみておくとすれば
図左は、円の中心に効用を最大とする飽和点を持っています。
例えば、日々の晩酌での X財=ビール、Y財=日本酒 でどうでしょう。
各々適量が一番です。
そして設問では、図右のようにして最適消費点を問われるでしょうか。
答えは、点A。当然、飽和点の効用が最も高くなります。
5.応用論点
最後にこの分野の応用論点を簡単にみておきます。
(1)消費と余暇の選択モデル
【出題~H25問14 H20問18】
このモデルは、『賃金と労働供給の関係』を調べようとしています。
図左から代替効果や所得効果を問われるくらいなら、特別なことは何もありません。むしろ、余暇の時間は上級財の仮定でしょうし、制約線もY切片しか動かないため、パターンが狭まっているほどです。
代替効果と所得効果の大小比較から労働供給曲線の形状は・・・
となってくると少々難しくなるかもしれません。
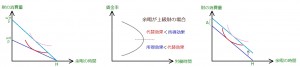
そのときは、結論として中央の図(後方屈曲的労働供給曲線)の形状を答えさせるような設問となるでしょうか。
それとも、あらかじめ中央の図を示し、図に書き込んだような代替効果と所得効果の大小比較を問われるか。
一応、想定できる変化として図右をあげておきます。
Aという不労所得を得たときのものですが、余暇時間の最大値は増やせないため、途中で途切れたような制約線となっています。
設問では、不労所得を得ると労働供給は減少しますよ、と結論付けてくるでしょうか。平成20年問18設問2を単純にしたようなものです。
(2)二期間消費モデル
【出題~H25問13 H22問2 H19問16】
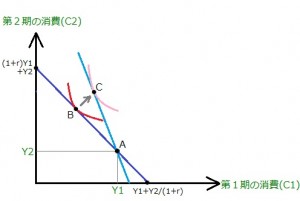
このモデルは、家計を二期間(若年期、老年期)に分けて考えています。
そして所与の利子率(r)において、各々の期間に得られる所得(Y1,Y2)をどのように分配し消費(C1,C2)するのが最も満足できるか、というようなことを調べています。
平成19年問16で、グラフ無しでこれをやるという暴挙に出ています。
平成25年問13も、制約線のY切片と傾きの数式を問うという、意図をはかりかねるような設問となっています。
要するに、これが絡むとろくな事にならないようです。
あまり関わらない方がよろしいのでしょうが、一応想定しているものを。
これに政府の行動を組み入れて『リカードの等価定理』というものを説明できるのですが、そこまではしなくても、何らかの形でその概念を選択肢に絡ませてくるようなことがあってもと。平成25年問8の雰囲気ですが、このあたりのお話がまたどこかで出てくるような・・・
今回は、以上です。
それでは、また。 Xレイ
※追記~質問の回答
ご質問ですがおそらくレポート課題は
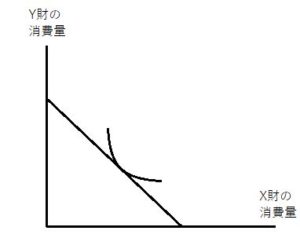
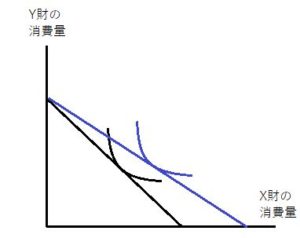
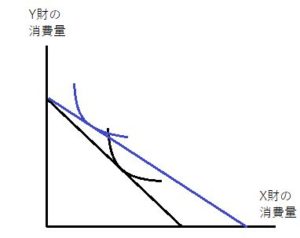
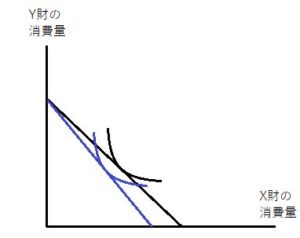
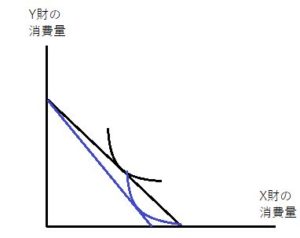
X財の価格Pxが下落、上昇したとき、X財が上級財、ギッフェン財それぞれの場合について予算制約線と無差別曲線はどう変化するか?
同様に、Y財の価格Pyが下落、上昇したとき、Y財が上級財、ギッフェン財それぞれの場合について予算制約線と無差別曲線はどう変化するか?
こんなところではありませんか?
以下、X財の場合についてその回答を。
上図を基本図として、各々変化後を青線で図示すると
このようになります。
Y財の変化も同じ要領で、グラフはX財のものを左右反転かつ時計回りに90度回転した形状となります。
この辺りはご自身でご確認願います。
以上、求めている回答でなかった場合はすみません。
Xレイ




松下さん
ご質問の回答ですが、本記事に追記したのでご覧ください。
こんにちは。現在大学生のものです。
レポートで、価格Pxが下落、上昇したときの上級財とギッフェン財の需要曲線の図と消費Pyが下落、上昇したときの上級財、ギッフェン財の需要曲線の図を書かなければならないのですが、自分で書いたものに自信がありません。もしよろしければ、これらの図を書いたものがあれば、教えていただけないでしょうか?