【渾身！論点シリーズ】経済学・経済政策　個人の消費行動分析②

こんにちは、たかじんです。

前回の記事では、個人消費行動の分析ツールとして、無差別曲線について解説しました。本日は、個人の消費行動分析において、無差別曲線とペアで使うツールである予算制約線について解説します。

 

何かモノやサービスを購入する場合、いくらでも際限なく買えるのであれば、効用（満足度）は増加していきます。もちろん購入量が増えていくほど、得られる満足度の増加量はだんだん減っていきますが（限界効用が逓減していくということですね）、それでも増加はしていきます。しかしいくらでもモノが際限なく買える、というような贅沢な状況は普通あり得ませんよね😅。

 

何かのモノ・サービスを購入する際には、現実の世界でも必ず「予算」が存在します。「海外旅行に行きたいけど、新車も購入したいなあ・・・」と考えた時、一番の制約になるのは、「いくらお金が使えるのか？」ということですよね。「海外旅行にも行けるし、新車も買える」という懐具合に余裕のある人以外は、どちらを選んだ方が満足度が高いのか、ということを考えて選択することになります。

 

経済学で個人消費分析を行う時も、モノ・サービスの購入に使えるお金の量には上限があり、その中で最も満足度が高くなるようにモノ・サービスの購入を行う、と考えます。

現実的には何も買わず、もしくは買う量を減らして残りは貯金するとか、借金をして予算以上のモノ・サービスの購入を行う、という選択肢もありますが、ここではモデルを単純にするため、貯金や借金を行わず、現在手元にあるお金を予算限度額いっぱいまで使って、モノ・サービスを購入するという前提を置きます。

もし貯金や借金の考え方まで入れると、現時点で購入する財の組み合わせだけでなく、将来的に購入する財の組み合わせも考慮して最適な消費行動を考えないといけなくなるため、モデルが複雑になってしまいますね。

 

さて、モデルを単純にするためのもう一つの前提として、この世に財はXとYの2種類しかないと仮定します。ある人が決まった額のお金を持っている時、XとYはどのように購入されるでしょうか。

 

ここで、X財の金額をPx、Y財の金額をPyとし、決まった額のお金、つまり予算上限をBとしましょう（Budget：予算の頭文字を取りました）。

X財をX単位分購入し、Y財をY単位分購入した時に必要な金額は、
Px・X＋Py・Yとなります。ちなみにPx、PyとX、Yの間にある「・」は積、つまりかけ算をしているという意味です。

この金額が予算上限であるBを上回ってはいけないので、
Px・X＋Py・Y≦Bが成り立ちます。

 

先程、この人は予算を余らせて貯金するということは考えない、つまり手元にあるお金を予算限度額まで使うという前提を置きましたので、

Px・X＋Py・Y＝B（①）が成り立ちます。

 

ではこの式をグラフに表すとどうなるでしょうか？

 

X軸、Y軸の二次元のグラフで表現する場合、一次関数であれば、Y＝a・X＋bの形で表現できます（きゃっしいさんの過去記事を参照して下さい）。

 

そこで、①の式をY＝a・X＋bという形に直すと、
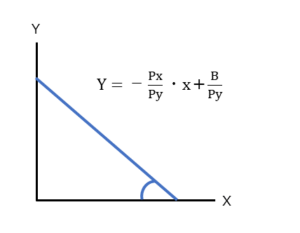
Y＝－Px/Py・X＋B/Py（②）となります。

これは傾き（Xの係数）がマイナスなので、右肩下がりの下記のような形のグラフになりますね。

この時、それぞれX軸、Y軸の切片はどうなりますでしょうか（ちなみに切片とは、グラフとX・Y座標軸の交点のことを指します）。

まずX軸の切片を見てみましょう。

X軸の切片は、Y＝０の時ですから、②のYに０を代入すると、
０＝－Px/Py・X＋B/Pyですから、Px/Py・X＝B/Pyとなり、両辺にPyをかけると、
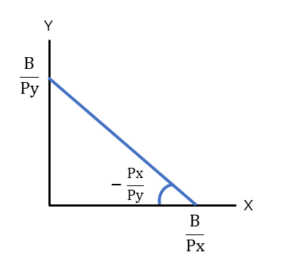
Px・X＝B、つまりX＝B/Pxとなります。

予算上限であるBをX財の値段であるPxで割っているので、これは予算全部を使って購入できるX財の量を表しています。

 

次にY軸の切片を見てみましょう。

Y軸の切片は、X＝０の時ですから、②のXに０を代入すると、
Y＝－Px/Py・０＋B/Pyですから、Y＝B/Pyとなります。

予算上限であるBをY財の値段であるPyで割っているので、これは予算全部を使って購入できるY財の量を表しています。

 

ではグラフの傾きはどうでしょうか。

グラフの傾きは②の式（Y＝－Px/Py・X＋B/Py）におけるXの係数部分ですから、－Px/Pyですね。符号がマイナスなので、右肩下がり（Xが増えればYが減るという関係）であり、PxをPyで割っているので、Px（X財の価格）のPy（Y財の価格）に対する割合を意味しています（前回の記事でも記載しましたが、「～に対する割合」という表現に出会った場合は、「～に対する」の直前に来ている言葉が必ず分母になります）。

さてこの予算制約線の式（Y＝－Px/Py・X＋B/Py）をもう一度見てみましょう。
登場するのは、以下の5つの要素です。

B：予算上限
X：X財の購入量
Px：X財の価格
Y：Y財の購入量
Py：Y財の価格

このうち、B、Px、Pyの３つの要素が変化すると、グラフの形状が変化します。
ちなみにB、Px、Pyが変化せず、XとYだけが変化する場合は、同じ予算上限のもとで、X財とY財の購入量の配分を変えるということですから、同一の予約制約線上を動くだけですので、グラフの形状は変わりませんね。

 

Bが変化した場合

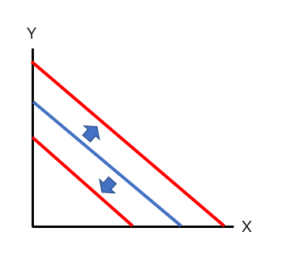
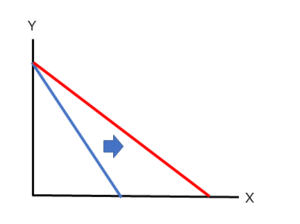
Bが大きくなる、つまり所得・収入が増大して、使えるお金が増えた場合はどうなるでしょうか。

グラフの傾きを表す－Px/Pyは変化しませんね。

一方、X軸、Y軸の切片である、B/Px、B/Pyの分子が大きくなりますので、B/Px、B/Pyとも大きくなります。
グラフの傾きは変わらないままで、X軸およびY軸の切片が大きくなりますので、グラフは外側に平行移動します（下記グラフにおける上方の赤い線に移動します）。

 

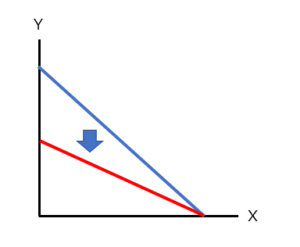
Bが小さくなる、つまり所得・収入が減少して使えるお金が減った場合は、この逆のことが起こります。

つまり、X軸、Y軸の切片である、B/Px、B/Pyの分子が小さくなりますので、B/Px、B/Pyとも小さくなります。
グラフの傾きは変わらないままで、X軸およびY軸の切片が小さくなりますので、グラフは内側に平行移動します（下記グラフにおける下方の赤い線に移動します）。

 

PxまたはPyが変化した場合

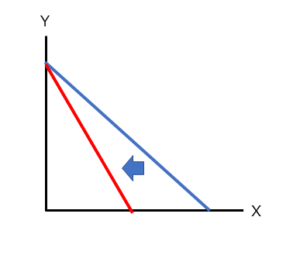
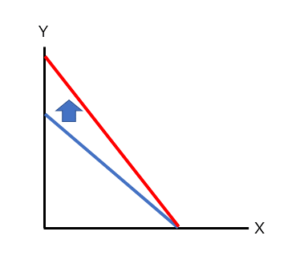
X財の価格が上昇、つまりPxが大きくなった場合はどうなるでしょうか。
グラフの傾きを表す－Px/Pyの分子が大きくなりますので、－Px/Pyの絶対値は増加し、グラフの傾きは急になります。
Y軸の切片であるB/Pyは変化しませんが、X軸の切片であるB/Pxの分母が大きくなりますので、B/Pxは減少します。すると、下記グラフのように変化します。

では、X財の価格が下降、つまりPxが小さくなった場合はどうなるでしょうか。
グラフの傾きを表す－Px/Pyの分子が小さくなりますので、－Px/Pyの絶対値は減少し、グラフの傾きは緩やかになります。
Y軸の切片であるB/Pyは変化しませんが、X軸の切片であるB/Pxの分母が小さくなりますので、B/Pxは増加します。すると、下記グラフのように変化します。

次にY財の価格が上昇、つまりPyが大きくなった場合はどうなるでしょうか。
グラフの傾きを表す－Px/Pyの分母が大きくなりますので、－Px/Pyの絶対値は減少し、グラフの傾きは緩やかになります。
X軸の切片であるB/Pxは変化しませんが、Y軸の切片であるB/Pyの分母が大きくなりますので、B/Pyは減少します。すると、下記グラフのように変化します。

次にY財の価格が下降、つまりPyが小さくなった場合はどうなるでしょうか。
グラフの傾きを表す－Px/Pyの分母が小さくなりますので、－Px/Pyの絶対値は増加し、グラフの傾きは急になります。
X軸の切片であるB/Pxは変化しませんが、Y軸の切片であるB/Pyの分母が小さくなりますので、B/Pyは増加します。すると、下記グラフのように変化します。

それでは消費者にとって最適な消費行動はどのように決まるのでしょうか。

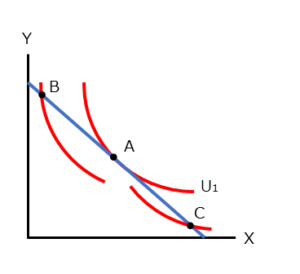
消費者は、限られた予算の中で、最大の効用を得られるように、モノ・サービスの購入を決定します。この点を最適消費点と言いますが、可視化するために、前回解説した無差別曲線と予算制約線のグラフを組み合わせてみましょう。

この時、無差別曲線と予算制約線の接点となる点Aが最適消費点となります。

例えば点Bでの効用を見てみましょう。点Bは点Aと同じ予算制約線上にありますが、点Aに近づくにしたがって、効用は高くなります。点Cでも同様に、点Aに近づくにしたがって、効用は高くなります。

つまり、同じ予算制約線上であれば、無差別曲線と交差する点ではなく、接する点が最適消費点となります。この時、予算制約線の傾きである－Px/Pyの絶対値と無差別曲線の傾きの絶対値であるMRS（Marginal Rate of Substitution：限界代替率）は一致します。

 

さてここまで見てきたところで、過去問を見てみましょう（前回同様、以下の過去問はすべて「一般社団法人中小企業診断協会」のホームページからの転載です）。

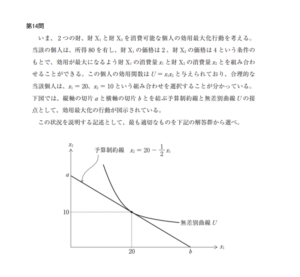
平成27年度の第14問です。

 

 

いかがでしょうか。

最適消費点は予算制約線と無差別曲線が接している、x1＝20、x2＝10のポイントとなります。ではそれぞれの選択肢を見ていきましょう。

ア：

現行の最適消費点よりも効用を高める余地が残されている、と記載されていますが、予算制約線と無差別曲線の接点以外の予算制約線上の点は最適消費点ではないので、間違いですね。

イ：

財X2の消費がゼロだとすると、予算制約線のx2に０を代入すると、x1は40となりますので、間違いですね。

ウ：

縦軸の切片は財X2の価格に応じて変化するため、これも間違いです。

エ：

無差別曲線上の組み合わせは効用はすべて一緒です。x1＝20、x2＝10とすると、効用関数U＝x1・x2に代入すると200となりますので、これが正解ですね！

 

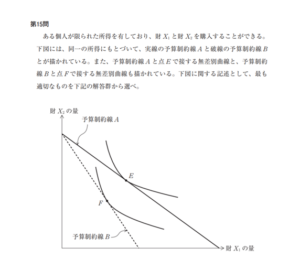
続いて平成28年度の第15問です。

 

いかがでしょうか。
こちらも簡単な問題ですね。解答はエですね！

それぞれの選択肢を見ていきましょう。
ア：

点Ｅと点Ｆでは、点Fの効用の方が低いので、間違いですね。

イ：

予算制約線AとBを比較するとBの方が財X１の価格が高いことを示していますので間違いですね。

ウ：

予算制約線Aの方が外側にあるため、実質所得は高いです。よって間違いですね。

エ：

これが正解です。予算制約線ＡとBとでは、傾きが変わっていますので、両財の相対価格が変化しています。予算制約線Bの方が傾きが急、つまり－Px/Pyの絶対値が大きくなっているので、Pxの価格が相対的に高くなっているか、Pyの価格が相対的に安くなっているかのどちらかです。

 

次回は個人の消費行動分析のラストとして、頻出論点の所得効果・代替効果について解説したいと思います。

 

以上、たかじんでした。
それではまた。