【渾身!論点シリーズ】個人の消費行動分析①
☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆
「お気に入り」「ブックマーク」にご登録ください!
☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆
こんにちは、たかじんです。
さて「渾身シリーズ」の今日のテーマは、経済学・経済政策でほぼ毎年出題されている「個人の消費行動分析」です。
個人の消費行動を分析するには、無差別曲線と予算制約線を使います。これらは「個人が限られた所得の中で、満足度を最大化するために、購入するモノやサービスをどう組み合わせるか」という個人の消費行動を考える際に使うツールです(無差別曲線と予算制約線の両方について記事を書くと、膨大な量になってしまうので、本日は無差別曲線に焦点を当てます。予算制約線については、また次回の記事でご説明します)。
さて実際の人間の消費行動は、非常に複雑ですし、決して合理的には動きません(いわゆる衝動買いってやつもありますし)。そのような複雑な現象を分析するのにあたり、いくつかの合理的と考えられる前提を置いて、エッセンスだけをモデルとして取り出して分析したのが経済学における個人消費分析です。
初めて経済学を学ぶ方には、「こんなに前提だらけで現実離れしたようなシンプルなモデルを分析して、一体、現実の世界でどう役に立つの?😩」と思われる方も多いと思います。
私も一応経済学部出身なので、擁護意見を言わせていただくと、「複雑な事象から本質(エッセンス)を抜き出す」、「多くの複雑な事象を抽象化・一般化する」、「スプレッドシートを使ってモデリングを行い、感度分析等が出来る」といった思考やスキルが身につく、といった効果があるのではないかと感じております。
そういえば物理を学ぶ時も、最初はいろいろな前提を置いて考えましたよね。摩擦が無いと仮定したり、天秤棒の太さは一様で、それ自体の重さは考えなかったり・・・。複雑な事象を分析するために、エッセンスを取り出して考える、という思考方法は一緒ですね!
・・・まあそんな御託を並べても、結局、試験科目にあるのだから勉強せざるを得ないのですが、苦手な方は、人生において決して無駄ではない、と自分に言い聞かせながら学習しましょう😅。
消費者の選好(Preference)について
さて個人の消費行動を分析するには、消費者の選好(Preference)について、以下の3つの前提を置きます。「選好」とはAとBというモノやサービス(経済学では「財(Goods)」と言います)があった時、どちらか一方を、他方より好んで選択する、という意味です。
①完全性・網羅性(Completeness)
消費者はAとBという2つのモノ・サービスを目の前に並べられた時、Aの方が良い、Bの方が良い、AとBはどちらを選んでも同じ、というように、どんな財でも必ずランク付けできるという前提です。
②推移性(Transitivity)
Aの方がBより良い、Bの方がCより良い、といった場合には、必ずAの方がCより良い、という結論になるという前提です。ジャンケンみたいな堂々巡りにならないようにするという前提です。
③「多い」方が「少ない」方より好ましい
モノにしてもサービスにしても、消費者は必ず多い方を好む、という前提です。
無差別曲線(Indifference Curve)
消費者の選好に基づく効用(Utility)をグラフの形で表したものが「無差別曲線」です。「効用」というのは簡単に言えば、いろいろな財を組み合わせて消費することから得られる「満足度」です。
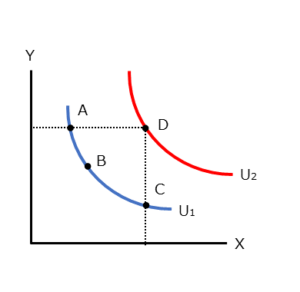
簡単なモデルにするため、世の中には選択できるモノ・サービスが2つ(XとY)だけあったと仮定します。同一の無差別曲線上(U1)にある2つのモノ・サービスに対する消費の組み合わせ(A点・B点・C点)は、当該の消費者にとって、すべて同じ効用(満足度)をもたらすと考えます。
なおこの曲線が右上にシフトした曲線(U2)の上にあるD点は、A・B・Cと比べて、それぞれ消費できるXとYが多くなっているため、上述の前提③によって、U2の方がU1よりも効用(満足度)が高くなっています。無差別曲線は原則、右上にシフトする程、効用(満足度)が高くなります。
ちなみに無差別曲線は英語で「Indifference Curve」と言います。「Indifference」とは、「違い」という意味の「Difference」に否定の接頭辞「In」が付いている言葉ですから、「違いが無い」という意味ですね。もちろん無差別という意味もありますが、どの点を選んでも効用は変わりないという意味では「中立」、「均等」、「どっちでも構わない」という意味を取って、「(効用)中立曲線」とか訳した方がニュアンスが伝わりやすいような気がします。
私見ですが、「無差別」って何となく「手あたり次第」とか「何でもかんでも」というニュアンスに感じ取れるので、「ムサベツキョクセン」と聞いても意味が余計分かりにくくなるような気がします。
余談ですが、経済学の用語はどうも変な和訳が多いような気がしますね。普通、「財」なんて言わないでしょ?でも「Goods」と言われれば、「ああ、『モノ』のことね」と分かると思うのですが・・・。
それはさておき、この無差別曲線の形状ですが、XとYというモノ・サービスを消費することから得られる効用を一定とすると、Xというモノ・サービスをx単位多く消費することが出来れば、その代わり、Yというモノ・サービスをy単位犠牲にしても構わないと想定することから、通常は原点に対して凸の形になります。
もしXをx単位多く消費したのにも関わらず、Yは今までと同じ量だけ消費できるのであれば、単にXをx単位だけ多く消費することが出来るようになっただけで、満足度は向上しますよね。すると「効用は一定」という前提が崩れてしまいます。
さて、この1単位あたりのXを、何単位のYで置き換えるかという割合のことを、限界代替率(Marginal Rate of Substitution:MRS)と言います。
より正確には、「XのYに対するMRS」と言い、追加で1単位のXというモノ・サービスを得るために、当該消費者が、Yというモノ・サービスを放棄することを許容できる最大の単位数、ということになります。もし「XのYに対するMRSが4」であれば、当該消費者は、Xを追加で1単位獲得するためには、Yを4単位放棄しても構わないと考えている、という意味です。
このようにMRSは、X軸(横軸)のモノ・サービスを1単位獲得するために、放棄してもよいY軸(縦軸)のモノ・サービスの単位、と定義されます。
これを数式にすると、
という形になります。X軸のモノ・サービスの効用がY軸のモノ・サービスの効用の何倍あるか、ということですね。
先程の例では「XのYに対するMRSが4」でしたので、X軸のモノ・サービスの効用がY軸のモノ・サービスの効用の4倍あるということになります。
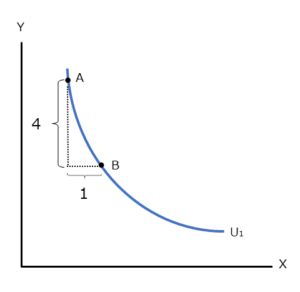
つまり下図の無差別曲線において、点Aから点Bに推移するにあたって、X軸のモノ・サービスを1単位獲得する代わりにY軸のモノ・サービスを4単位放棄しても、当該の消費者にとって得られる効用は変わらないということです。なお、下記のグラフはMRSを視覚的に理解するために作図したもので、あくまでもイメージ図です。厳密には、MRSは無差別曲線の接線の傾きの絶対値になります(もうひとつ下のグラフをご覧下さい)。
よく経済学や財務会計では「〇の△に対する~」という言い方がよく出てきます。これは何らかの割合を表現している言い方です。
「割合」というからには何かを何かで割っているのですが、この時、どっちが分母でどっちが分子なのか、混乱する時はないでしょうか。
もし混乱しやすい場合は、常に「~に対する」という言葉に注目しましょう。「~に対する」の直前に来ている言葉が必ず分母になります。「XのYに対する」と書かれていた場合は、Xが分子でYが分母です。先ほどの「XのYに対するMRS」という場合、Xの効用をYの効用で割っている、つまり分子が「Xの効用」で、分母が「Yの効用」ですよね。需要の価格弾力性という言葉も、言い換えると「需要の価格に対する弾力性」ということですから、価格の変化が分母に来ます。
さてこのMRSですが、通常はXが大きくなるほど、逓減していきます。「逓減」という言葉も経済学独特の言い回しですが、要するに「徐々に減っていく」ということです。
Xが手元に少なく、Yが手元に多い時は、Xを追加で1単位得ることの価値が相対的に大きいため、Yを多めに失ってでもXを追加1単位得たいと思いますが、Xがだんだん多くなって、Yが少なくなってくると、Xを追加で1単位得ることの価値が相対的に低下していきます。これはMRSがXが大きくなるにつれて、小さくなることを意味しています。したがって、傾きが徐々に小さくなっていくため、無差別曲線の形は原点に凸になっていくと想定されるのです。
下のグラフでは点A→点B→点Cに行くにつれて、無差別曲線の傾き(つまりMRS)が徐々に小さくなっていくのが見て取れるかと思います。
ところが、モノ・サービスの組み合わせによっては、このMRSが独特の動きをするため、無差別曲線の形状が原点に凸にならない場合があります。
無差別曲線の形は基本的にMRSがどのように変化するかで変わります。
MRSが一定のケース
MRSが一定ということは、無差別曲線の傾きが常に一定ということになりますから、以下のような形状になります。
これはXを追加1単位得るために、Xが手元に少ない時や多い時に関わらず、放棄してもよいYの単位が一定ということを意味しており、XとYが完全に代替の関係にあるケースです。例えば、出光から買うガソリン1ℓとエクソンモービルから買うガソリン1ℓは、消費者にとって、まったく同じ価値です。出光から買ったガソリンが手元に少ないからといって、追加で出光から1ℓのガソリンを購入するのに、エクソンモービルから買ったガソリンを2ℓとか3ℓとか放棄して手に入れませんよね。どちらも同質の製品です(出光佐三を尊敬しているから、出光のガソリンの価値を高く感じる、というような特殊な方がいらっしゃるかもしれませんが、これは脇に置いておいて)。このような関係にあるモノ・サービスを「完全代替財(Perfect Substitutes)」と言います。
MRSがゼロのケース
横軸にとったモノ・サービスがいくら増えても、消費者の効用に無関係な時、MRSの分子であるX軸のモノ・サービスの効用はゼロであり、MRS=0となりますので、横に水平な無差別曲線(傾きが0の直線)が描かれます。
MRSが無限大のケース
縦軸にとったモノ・サービスがいくら増えても、消費者の効用に無関係な時、MRSの分母であるY軸のモノ・サービスの効用はゼロであり、MRS=∞となり、縦に垂直な無差別曲線(傾きが∞の直線)が描かれます。
MRSがL字型のケース
これはMRSが0のケースと無限大のケースの組み合わせとして表示されます。
あるポイントを超えると、MRSが0になったり無限大になったりするケースです。手袋とか靴のように、ペアで揃っていないと意味が無いモノが、よく例として挙げられます。
X軸が右足用の靴の数量、Y軸が左足用の靴の数量とした場合、右と左、ひとつずつあれば充分なのですが、もし右足用の靴がふたつ、みっつと増えていっても、使えませんので、X軸に取ったモノ・サービスがいくら増えても消費者の効用に無関係ですから、MRS=0となり、水平な無差別曲線となります。反対に、左足用の靴がふたつ、みっつと増えて行っても、これも使えませんので、Y軸にとったモノ・サービスがいくら増えても消費者の効用に無関係ですから、MRS=∞となり、縦に垂直な無差別曲線となります。このような関係にあるモノ・サービスを「完全補完財(Perfect Complements)」と言います。
MRSが逓増のケース
Xというモノ・サービスが手元に少ない場合、追加で1単位を得るために、失ってもよいYというモノ・サービスは1より少なく、Xが手元に多くなってくると、失ってもよいYの量が増えてくるというケースです。
そんなケースって現実的にあるのか?という感じですが、XとY、両方を消費するよりは、どちらか一方のみを消費したい場合はこのような形になります。直感的には、どちらか一方の財のみを消費したい場合、なかなかそのポジションから動かず、もう一方の財はあまり増やしたがらないけれども、ある一点を超えると、もう一方の財の消費に急速にシフトしていく、というような感じでしょうか。
例えば、iPhoneを使用している消費者は、手元のスマホの2台目、3台目として、なかなかAndoridのスマホを採用したがりませんが、手元のスマホの台数のうち、Androidの方が多くなってくると、全部Androidにしてしまった方が満足度が高いので、急速にAndroidに舵を切る、というようなシチュエーションでしょうか(余計分かりにくい?)。
その他の特殊ケース
円型の無差別曲線
ふたつのモノ・サービスの組み合わせのうち、最適な組み合わせがたった一つだけ決まる場合には、円型の無差別曲線になります。
例えば、晩酌にはビール2本と日本酒2合を飲むのが最適だという人がいた場合、下記のようなグラフになります。ビール1本と日本酒3合だと、翌日二日酔いになってしまうとか、ビール3本と日本酒1合ではちょっと物足りない、というような場合でしょうか(下のグラフの場合の効用は、他のグラフと違ってU1>U2になっています)。
ふたつのモノ・サービスのうち、他方の増加が好ましくない場合は下記のようなグラフになります。よく挙げられる例としては、所得と労働時間の組み合わせとか、所得とゴミの量の組み合わせとかがあります。この場合は左上に行く方が効用(満足度)が高くなります。
さてこれで無差別曲線については、理屈とすべてのケースを網羅しました。
ここで早速過去問を解いてみましょう(以下の過去問はすべて「一般社団法人中小企業診断協会」のホームページからの転載です)。
まず平成27年度の問題です。
完全補完財の無差別曲線はどれか、という問題です。
簡単ですね、答えは図Bです!
図Aは普通の無差別曲線、図Cは完全代替財(MRSが一定)、図DはMRSが逓増する財のケースでした。
では続いて平成29年度の問題です。
MRSが無限大になっているケースです。MRSが無限大と言うことは分母がゼロ、つまりY軸に取られている財の効用がありません、というケースですね。
答えは、そう、ウですね!
アは完全補完財ですね。コーヒー1杯について、角砂糖1個だけ入れます。それ以上はコーヒー、角砂糖、どちらが多くても満足度は上がりません。
イは完全代替財です。
ウはY軸の財(野球のチケット)の効用がゼロですので、これが答え。
エは問題文が分かりにくいですが、パンとおにぎりで代替性があり、完全代替財という訳ではなさそうです。これ以上の記述が無いので、普通の無差別曲線だと思われます。少なくとも垂直に立っている無差別曲線ではないですね。
本日は無差別曲線についてのみご説明しましたが、これだけでは個人消費の分析は出来ません。次回は予算制約線について書きたいと思います。
以上、たかじんでした。
それでは、また。


-e1525574405866-300x234.png)
-e1525574065337-300x257.png)
-e1525574039232-300x247.png)
-e1525574141718-300x245.png)
-e1525574112222-300x249.png)
-e1525574089484-297x300.png)
-e1525574166718-300x264.png)
-e1525574192163-300x275.png)
-e1525574255658-218x300.png)
-e1525574229644-215x300.png)

「現実の世界でどう役に立つの?」のくだりがとても面白かったです。
「たしかに科学の実験も温度が一定で、ノイズがない環境なんて現実にはないなぁ」と思いながら興味深く読ませていただきました。
自分にとって、このような興味や納得感はモチベーションに繋がるのでとても助かりました。
素敵な記事をありがとうございます。
あいさん
こんにちは、たかじんです。
コメントいただきましてありがとうございました!大変励みになります!
私も経済学を初めて勉強した時に、「モデルの分析が何の役に立つのだろう?」と思ってましたので、雑感として書かせていただきました。
現実の世界はノイズが多いので、政府の経済政策は必ずしも思った通りの成果には結びつかないことも多いですが、「全体的にはこういう方向に動くはず」という仮説を持って動くのと、そういう理論的な仮説もなく動くのとでは、たとえ同じ結果になったとしても、プロセスをきちんと検証できるかどうかという大きな違いが出て来ると思います。これは企業経営でも同じですよね。
一次試験まであと3ヶ月を切っておりますが、あいさんの合格を祈念しております!