【渾身?】経済学・経済政策vol.2~IS‐LM分析~
おはようございます。フェイマオです![]()
6月も後半に入り、今週から関東地方でも梅雨らしい天気に入ってきました![]()
大雨の影響を受けていらっしゃいます九州地方の皆様、くれぐれもご注意くださいませ![]()
私事ですが嬉しい事に(?)、最近仕事がかなり忙しくこのブログも6/21の23時半から書かせて頂いており、かなり新鮮な記事でございます(笑)![]()
先週末で、恒例の【渾身】シリーズは終了致しましたが、前回に引き続き“経済ネタ”をお送り致します![]()
さて、この経済学という科目は財務会計と並んで比較的苦手とする受験生の方がいらっしゃるかと思います。
前回の記事でもお話をさせて頂きましたが、(個人的には)マクロ経済学はミクロ経済学に比べて問題が難しく作りやすい科目だと思います。
“(答えを導くのに必ずしも必要のない)難解な数式を用いる”事や、“「弾力的・非弾力的」といった普段馴染みのない語句を用いる”などして、受験生を惑わせるには『もってこい』な科目だと感じています。
私フェイマオの個人的な意見ではありますが、マクロ経済の範囲は“暗記”に頼ってしまうと、やや危険かもしれません![]()
試験初日の1発目の科目という事もあり緊張感が高まっている中で、「覚えていたことが(瞬時に)引き出せない」とパニックを起こしてしまううえ、続く財務会計以降の科目にも影響が・・・![]()
でも、安心してください![]()
少なくともマクロ経済の分野は、IS-LM分析(マンデル=フレミング・モデル含む)まで一通り理解出来たら、後のパートは暗記でも対応可能だと思います。
さて、今回はIS-LM曲線分析では有名な『クラウディング・アウト』について![]()
クラウディング・アウトがどんなものかは、既にご存知かと思いますが一言でいうとこんな感じ。
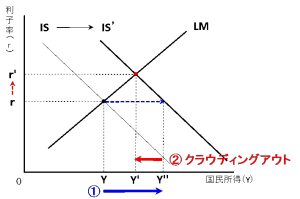
そして、テキストでよく見る図がこちら。
上記の図で、利子率が変わらない場合、財政政策を発動すると(政府支出の増加)、IS曲線がIS’曲線へと右シフトして、国民所得がY’’となります。(上記図の①)
しかし、IS曲線とLM曲線の同時分析の場合には、『利子率が一定でない』ため、政府支出の増加分ほど国民所得が増加せず減少(Y’’→Y’)してしまいます(上記図の②)
これだとかなり大雑把な説明ですが、このクラウディング・アウトは『IS曲線の動き⇒LM曲線の動き⇒IS曲線の動き』に分解して考えると、理解しやすいかと思います。
上記に記載した各曲線の動きについては、読者の皆様はご理解頂いているかと思いますので説明は割愛させて頂きます。
さてこの分解した式をご覧頂いて、『クラウディング・アウトを発生させないためにどうするか?』を考えてみてください![]()
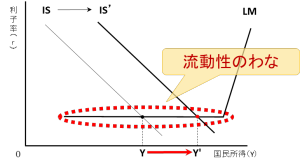
では、上で示した各曲線の動きを再掲した下の図をご覧ください。
実は、クラウディング・アウトの発生を防ぐには、上の図で点線で囲ったところがポイントです。
【1】の場合:『貨幣取引需要が増加しても利子率が変わらない・・・』パターン
→これは皆さんご存知の通り、“流動性のわな”の状態の時です。
※説明をだいぶ割愛してますので、この説明が必要な場合はコメントにご記載下さい。LM曲線の導出について図解させて頂きますm(__)m。
ご覧頂いてお分かりのように、LM曲線が水平の場合は、利子率が変わらないため投資が減少せず、結果的にクラウディング・アウトが発生しません。
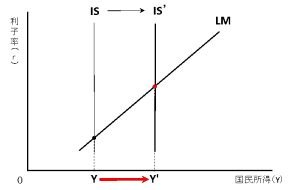
【2】の場合:『利子率が上昇せず、投資が減少しない・・・』パターン
→これは、投資が利子の影響を受けない=投資が利子非弾力的な場合ですので“IS曲線が垂直”の場合です。
では、なぜ投資が利子非弾力的だとIS曲線が垂直になるのか?
考え方は以下の2つでご説明します。
①前回の記事の“ち り”で考える
“投資が利子非弾力的”という事は、投資が利子率の変化に反応しないという事ですので、『投資の利子感応度がゼロ』という事です。
つまり、投資の利子感応度が限りなく小さいため、“IS曲線の傾きが限りなく大きくなる=垂直になる”のです。
②IS曲線の導き方から考える
下のグラフを見て頂くと、IS曲線の導き方が分かるかと思います。
左のグラフ:利子率が下がる→(お金を借りて)投資をする人が増える
中のグラフ:増加した投資量だけ、総需要曲線が上にシフトして国民所得が増える
右のグラフ:左のグラフの縦軸:利子率と中のグラフの横軸:国民所得をあわせると、IS曲線が出来る。
これを踏まえて、下のグラフをご覧ください。
つまり、左のグラフの投資曲線が垂直の場合にIS曲線も垂直になります![]()
IS-LM分析については、「それぞれの曲線がなぜそのように動くのか?」を理解して頂くためにも、是非ご自身で手を動かしながら、復習を進めてみてください。
では本日はここまで![]()
To be continued・・・